Trees Part 1
by Ron Penton

Introduction

Trees are a very important portion of software programming theory. Whether you know it or not, they are used all around you, in many applications and games. This is why it was quite a surprise to me when I found out that most of the programmers that frequent the GameDev.net chat room don't know exactly what trees are, and what they are good for. I hope this article will remedy that.

My original intent was to not provide any code for this tutorial, as I prefer it when people learn the theory rather than just copy the code (and probably use it for a computer science homework project), but I have come to realise that quite a few of you learn better by seeing an example of the topic rather than just an explanation. Therefore, I have included source code and demo programs to accompany this tutorial.

This specific tutorial briefly covers recursion first, because it is a very important topic to understand before you get involved with trees. The next part describes how a tree is structured and how parts of a tree are labelled, and the last part shows how to use a General Tree.

Basic Requirements for this series:

Knowledge of basic data structures:
Linked List
Stack
Queue
Priority Queue

Knowledge of basic C++ programming:
inheritance
templates
function pointers

Included Classes for this tutorial:

LinkedList
GeneralTree

Recursion

Trees are highly recursive structures. I'm hoping that you will be somewhat familiar with recursion as a theory, because it is a difficult subject to get correct for most beginning programmers. Here is a tiny introduction to recursion (you'll probably want to find a more in depth tutorial if you've never heard the term before).

What is recursion? An old programmers joke has the definition of Recursion in the dictionary as this:

re·cur·sion n.: See Recursion.

The basic idea behind a recursive function is one which calls itself repeatedly on many different levels. A recursive structure, such as a tree, has itself as its own children, and is thus considered recursive. Recursion helps software engineers solve problems by dividing up complex problems into smaller sub-problems, and is often a great boost in algorithm completion time, because recursion helps to "divide and conquer" the problem at hand, thus reducing the complexity. I will go into this further in the next tutorial dealing with binary tree’s.

The basic recursive function will have two portions: the recursive part, and the terminating part. It is very important that recursive functions have a terminating part, because without it, the recursive function would never end. The above joke is an example of recursion without a terminating condition. If it were in a program, the program would continuously look up the definition of recursion forever.

Of course, having a machine run into infinite recursion is just as deadly as an infinite loop, but the difference between the two is that infinite recursion will eventually cause the machine or thread to quit out. This is because each recursive call allocates more information on the stack every time it is called, and when the machine or thread runs out of stack space, it quits out.

The stack is the most important part of recursion. It is an easy way to have the machine store current state information about a function, change to another object, and then return at a later time. Let's look at a simple recursion example:

int getPower( int number, int power )
{
  if( power != 1 )
    return number * getPower( number, power - 1 );
  else
    return number;
}

Here is the non-recursive solution to the same problem:

int getPower( int number, int power )
{
  int result = number;
  while( power > 1 )
  {
    result *= number;
    power--;
  }
  return result;
}

While the recursive example looks ugly and stupid, and the iterative example is far more efficient, it demonstrates an important idea behind recursion. The terminating case is where power is 1. When power reaches 1, it returns a number instead of calling itself again. The recursive portion of the function decides to let the function handle the power one less than the current power, as long as the current power is not 1. So if the function were to calculate 2 to the Nth power, it would first check to see if N was one, and if it isn't, it asks for the solution to the problem of 2^(N-1), until it gets to 2^1, in which case it returns 2. If N were 2, it would ask for 2^1 and multiply that by 2, and return. If N were 3, it would ask for the solution to 2^2 and muliply that by 2. That is the basis of recursion.

So why use it? If analyzed, the recursive getPower function is slower and harder to understand than the non-recursive iterative solution, so it quite obviously offers no advantage. Recursion is not used to its full potential in this example simply because I wanted to show you how a problem can be broken down into a smaller problem by using recursion (Look for tutorials on The Towers of Hanoi problem for a really cool demonstration of this effect).

The real reason we would use recursion is for a simple way of storing values on a 'path' for future use. Recursion store's the state of the algorithm at each level and allows the user to come back to that exact state later on. We will see this in use when using the tree traversal routines.

Introduction to Trees

Trees are used for so much in computer programming. They can be used for improving database search times (binary search trees, 2-3 trees, AVL trees, 2-3-4 trees, red-black trees), Game programming (minimax trees, decision trees, pathfinding trees), 3d graphics programming (BSP trees, quadtrees, octrees), Arithmetic Scripting languages (arithmetic precedence trees), Data compression (Huffman trees), and even file system's (B-trees, sparse indexed trees, trie trees). This article will go through the basic tree structures first (general trees), and then go into the specifics of some of the more popular trees, but not all of those listed above. A few of the trees above are quite complex and go beyond the scope of this article.

Computer Representations of Trees

Imagine a linked list. The simplest implementation uses only one class, a Node, and each node points to the next node in the list. In more sophisticated implementations, the node may even point to the previous node in the list as well. This implementation treats any given node as the start of a list when accessed externally by the client. The more abstracted implementations use a general container class that points to its first node.

The box represents the Linked List class, and the circles are the nodes. Trees are the same way in that they are made up of a collection of nodes. As with linked lists, a tree can be referenced by any one of it’s nodes, or a general tree container class. Whichever implementation you choose is all up to you and your needs. This tutorial does not assume one particular way over another, but all tree diagrams I will draw in this document do not show the container (box) class for reasons of clarity and brevity. It looks better without the box getting in the way.

Parts of a Tree

Trees have one discrete starting point. This is called the root node. As with a linked list, each node points to another node, but the difference is that a tree node can point to more than one node, whereas a linked list node can only point to one node. Each of the nodes that any given node points to is called a child node, with the possible exception of a parent node. Some tree implementations maintain pointers to their parents to ease traversal, but it is not explicitly required by a tree. Any node that does not have any children is called a leaf node. Here is a pictorial representation of a theoretical tree:

Note that computer trees are typically drawn from the Root-down. Node 1 would be considered the root, and 2, 3, and 4 are children of the root. Node 1 is their parent. Note also that node 2 is a parent to 5 and 6, and 4 is a parent to 7. Thus nodes 2 and 4 act as both children and parents. Nodes 3, 5, 6 and 7 are leaf nodes. It is important to note that every node in the tree is also a tree by itself. We usually call these sub-trees. Take, for example, node number 2. Node 2 is the root of a sub-tree that only has three nodes. Node's 5, 6 and 7 are all sub-trees with no children.

Hierarchy of a tree

When you think of a linked list, it is typically a long horizontal string of nodes, each one connected to the next. This gives it a shape roughly analogous to a straight memory array. However, trees cannot be easily thought of in terms of a straight line, so a tree has what are called Height Levels. The root node has a level of 0 (or 1, depending on how you count), and all children of any given node have a height level of one greater than the parent. All children of any given node have the same height level.

Here is an example of height levels:

General Trees

The General tree (also known as Linked Trees) is a generic tree that has one root node, and every node in the tree can have an unlimited number of child nodes. One popular use of this kind of tree is in Family Tree programs. Here's an example family tree:

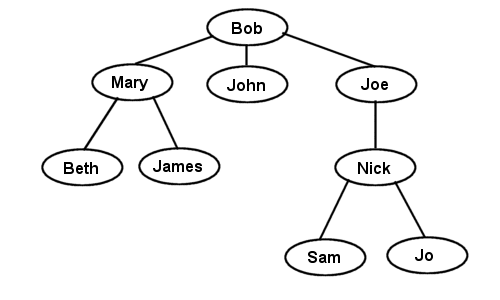
Any parent node is allowed to have as many children as it wants. (Random fact: Johann Sebastian Bach had 19 children). The standard method of representing a general tree is to use a linked list (hence the name linked tree) in each node to hold pointers to all of the children. You don't need to use a linked list though, you can just as easily use a resizable array, or any other linear container structure you can think of, but a linked list is usually the easiest way to think about storing the child nodes of a general tree. A representation of a Linked General Tree using the above family tree example would look like this:

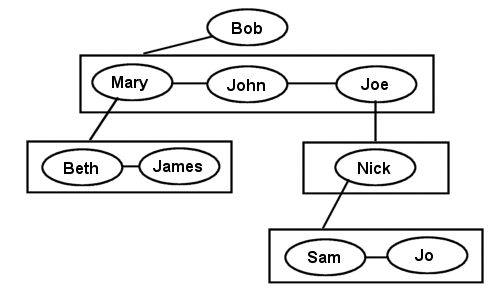
Each box is a linear container, and each node has a pointer to a single linear container.

Using The General Tree

So, what would you use a general tree for? In game programming, many games use these types of trees for decision-making processes. For example, a computer AI might need to make a decision based on an event that happened. Here's an example of a computer gunman thinking about what to do when he hears a gunshot:

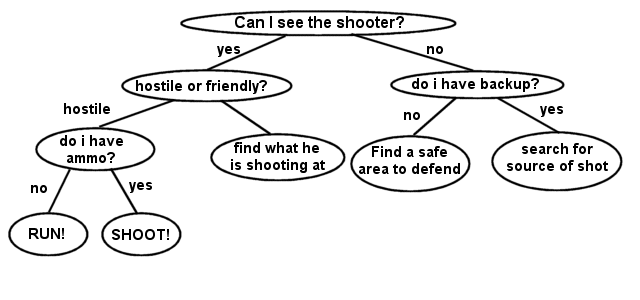
This is just a simple tree for demonstration. A more complex AI decision tree would definitely have a lot more options. The great thing about using a tree for decision-making is that the options are cut down for every level of the tree you go down, greatly improving the speed at which the AI makes a decision. Other uses might include storing level progressions. In level based games, there is a strong push lately to get rid of the old school "linear" line of thinking, and instead of using just a rigid number of pre-defined levels, maybe the level structure of a game might progress based on a tree. The big problem with tree based level progressions, however, is that sometimes the tree can get much too large and complex. Imagine offering just two choices for the next level at the end of each level in a ten level game. That would require a total of 1023 levels to be created. That requires quite a bit of effort, so it's best to try to limit the number of level choices. There are thousands of other uses for trees, and chances are there is something you want to do that trees are the best solution for.

The General Tree Interface

Here is a listing of the basic public GeneralTree interface that I have created:

Template <class dataType>
class GeneralTree
{
// ----------------------------------------------------------------
//  Name:           GeneralTree::GeneralTree
//  Description:    Default Constructor. Creates a tree node.
//  Arguments:      - data: data to initialise node with
//  Return Value:   None.
// ----------------------------------------------------------------
  GeneralTree( dataType& data );


// ----------------------------------------------------------------
//  Name:           GeneralTree::~GeneralTree
//  Description:    Destructor. Deletes all child nodes.
//  Arguments:      None.
//  Return Value:   None.
// ----------------------------------------------------------------
  ~GeneralTree();


// ----------------------------------------------------------------
//  Name:           GeneralTree::addChild
//  Description:    Adds a child node to the tree’s child list.
//  Arguments:      - tree: sub-tree to add
//  Return Value:   None.
// ----------------------------------------------------------------
  void addChild( GeneralTree<dataType>* tree );


// ----------------------------------------------------------------
//  Name:           GeneralTree::start
//  Description:    resets the child iterator to point to the first
//                  child in the current tree.
//  Arguments:      None.
//  Return Value:   None.
// ----------------------------------------------------------------
  void start();


// ----------------------------------------------------------------
//  Name:           GeneralTree::forth
//  Description:    moves the child iterator forward to point to
//                  the next child.
//  Arguments:      None.
//  Return Value:   None.
// ----------------------------------------------------------------
  void forth();


// ----------------------------------------------------------------
//  Name:           GeneralTree::isValid
//  Description:    determines if the child iterator points to a
//                  valid child.
//  Arguments:      None.
//  Return Value:   True if the iterator points to a valid child,
//                  False otherwise.
// ----------------------------------------------------------------
  bool isValid();


// ----------------------------------------------------------------
//  Name:           GeneralTree::currentChild
//  Description:    returns a pointer to the current child tree
//                  that the child iterator points to.
//  Arguments:      None.
//  Return Value:   pointer to current child tree
// ----------------------------------------------------------------
  GeneralTree<dataType>* currentChild();


// ----------------------------------------------------------------
//  Name:           GeneralTree::removeChild
//  Description:    removes the child that the child iterator
//                  is pointing tom and moves child iterator to
//                  next child.
//  Arguments:      None.
//  Return Value:   None.
// ----------------------------------------------------------------
  void removeChild();


// ----------------------------------------------------------------
//  Name:           GeneralTree::preorder
//  Description:    processes the list using a pre-order traversal
//  Arguments:      - process: A function which takes a reference
//                             to a dataType and performs an
//                             operation on it.
//  Return Value:   None.
// ----------------------------------------------------------------
  void preorder( void (*process)(dataType& item) );


// ----------------------------------------------------------------
//  Name:           GeneralTree::postorder
//  Description:    processes the list using a post-order traversal
//  Arguments:      - process: A function which takes a reference
//                             to a dataType and performs an
//                             operation on it.
//  Return Value:   None.
// ----------------------------------------------------------------
  void postorder( void (*process)(dataType& item) );
};

There is no default constructor, because a tree object MUST contain a piece of data. Therefore you are required to pass in a dataType to it on creation. Note that the destructor of a tree recursively delete’s all of it’s children, so when adding a sub-tree to a tree, make sure it is not referenced anywhere else in the program. The destructor, however, does NOT delete the data stored inside the tree node, so that must be managed by the client of the tree.

Since the tree will be using a linked list to store it’s children, the tree maintains a pointer (known as the iterator) to the current child. The basic iteration functions allow the user to reset the pointer to the start of the list (start()), travel through each child individually (forth()), retrieve the item at the current child iterator location (currentChild()), delete the current child subtree (removeChild()), and determine if the iterator is not pointing to a valid child (isValid()).

The Traversal methods will be discussed later on in this tutorial.

Adding Nodes to the General Tree

The most common way to add nodes to a general tree is to first find the desired parent of the node you want to insert, then add the node to the parent's child list. The most common implementations insert the nodes one at a time, but since each node can be considered a tree on its own, other implementations build up an entire sub-tree before adding it to a larger tree.

Example of adding nodes to a linked tree:

void main()
{
  GeneralTree<int>* tree = new GeneralTree<int>( 1 );
  GeneralTree<int>* temp = 0;

  tree->addChild( new GeneralTree<int>( 2 ) );
  tree->addChild( new GeneralTree<int>( 3 ) );
  tree->addChild( new GeneralTree<int>( 4 ) );

  tree->start();
  temp = tree->child();
  temp->addChild( new GeneralTree<int>( 5 ) );
  temp->addChild( new GeneralTree<int>( 6 ) );

  tree->forth();
  tree->forth();
  temp = tree->child();
  temp->addChild( new GeneralTree<int>( 7 ) );
}

This snippet creates the tree that was given as an example of a general tree earlier using Top Down construction, where the root is created first, and the children are added later. Another way would have been to create the children first and add the sub children to the root. Building order: create node’s 5 and 6, create node 2, add 5 and 6 to 2, create 3, create 7, create 4, add 7 to 4, create 1, and add 2, 3 and 4 to node 1. This method is called Bottom Up construction.

Removing Nodes from the General Tree

Removing a node is entirely dependant on the use of the tree. The typical method to remove a node from a general tree is to find the node you want to remove, and just delete it from the current list it is in (this is what the removeChild() function does). This will remove the entire sub-tree, however, and if you want to keep the removed node's children in the tree, its up to you to re-add them. Example of removing a sub-tree from the tree.

void main()
{
  GeneralTree<int>* tree = new GeneralTree<int>( 1 );

  // create tree used in previous example here
  // ...

  tree->start();
  tree->removeChild();
}

This removes the entire subtree starting at node 2, which ends up removing both nodes 5 and 6 from the tree as well. Note that this is the standard accepted behavior of a remove routine, since children of a node are assumed to be related to the parent in an important manner, and maintaining them in the tree without the parent usually does not make sense.

Processing Nodes in the General Tree

Often, there arises a need to perform one operation on every node of a tree. Therefore, we need to use a method that traverses the entire tree and visits every node. There are generally three traversal methods for trees that guarantee that every node will be visited, however only two of them are used for general trees. They are called the Pre-Order Traversal and the Post-Order Traversal. The third such traversal, In-Order, is usually only used on binary trees. These traversal methods are recursive functions, and demonstrate how useful recursion can be.

The Pre-Order Traversal works by processing the current node first, and then processing all the children, where process() may be any user defined function. The reason this works is because in recursion, I stated earlier that the computer remembers the current state of the tree, and even though processing goes down an unknown number of levels, you can be assuered that when processing returns to the first function, you can continue processing the tree as usual. The recursive algorithm looks like this:

template <class dataType>
void GeneralTree<dataType>::preorder(void (*process)(dataType& item) )
{
  process( m_data );
  start();
  while( isValid() )
  {
    currentChild->preorder( process );
    forth();
  }
}

So, printing the items of the family tree example above would produce the list: Bob, Mary, Beth, James, John, Joe, Nick, Sam, Jo. First it processes Bob, then processes each of his children. Mary is the first child, so she is processed and it goes down to the next level, where it processes Beth and James. Since they don't have children, it jumps back up to Mary, then sees she has no more children, and jumps up to Bob. It then processes Bob's next child, John, and continues with Joe. It is called Pre ordering because it processes the root node before the children. This traversal is also known as the Depth-First traversal, because it traverses one path all the way to the bottom before it comes back up and follows a different path.

Now, since Pre ordering processes the root node first and the child second, Post ordering processes the children nodes first, and the root node last. The recursive algorithm for this is:

template <class dataType>
void GeneralTree<dataType>::postorder(void (*process)(dataType& item) )
{
  start();
  while( isValid() )
  {
    currentChild->postorder( process );
    forth();
  }
  process( m_data );
}

Printing the items of the family tree using a Post-order would produce: Beth, James, Mary, John, Sam, Jo, Nick, Joe, Bob. If you have a firm grasp on recursion, this is quite easy to understand. If, however, this is all gibberish to you, I would suggest reading up on recursion, because in the next article, recursion is discussed more in depth, and you need to have at least a working understanding of the basic concepts.

Why recursion was used in these traversals

As I have said many times before, recursion is a powerful tool because it allows a large problem to be broken down into a much simpler problem. In the case of traversal, the beauty lies in being able to specify a small function which operates on only one node and allows the children to solve the problem for their children as well, thus allowing the root (or any parent node in the tree) to remain totally ignorant of the structure of its children. When you pre-order a tree, you process the root node, and then call preorder on each of it’s children. So when you preorder a child, it completes and pop’s execution back up to the root, allowing it to do the same thing to the next child, then the next, and so forth.

While it is possible to represent the traversal problem with an iterative solution, that solution would require a custom made stack, which is esentially using recursion with a different name. It is likely that the user defined stack will not be as efficient as the system stack, so an iterative solution would end up being slower.

The importance of recursion is somewhat downplayed in the traversal routines because each tree node maintains a pointer to the current child. Now, imagine a general tree implementation that used an array for its child list instead of a linked list. An array does not have an iterator object, and must use an index variable instead. In this case recursion helps because the index is stored on the stack at every level, and automatically restored when execution returns to each higher level. Recursion essentially helps the algorithm remember which path it traveled down.

In the end, recursion works so well with tree’s because a tree is esentially a recursive structure.

Conclusion

That's it for this tutorial. I had intended to include even more tree related stuff, all into one tutorial, but it ended up being too large. So next time, in part II, the tutorial will continue on with trees. Specifically, we'll be looking at binary trees, a specific subset of all trees, and the many various things that have been done with binary trees. I think I'll finish up at the third article, going into some of the more advanced tree structures. Until next time!

Discuss this article in the forums

Date this article was posted to GameDev.net: 5/27/2001
(Note that this date does not necessarily correspond to the date the article was written)

See Also:
Data Structures