The Physics of Racing, Part 10: Grip Angle

physicist and member of
No Bucks Racing Club

P.O. Box 662
Burbank, CA 91503

In many ways, tire mechanics is an unpleasant topic. It is shrouded in uncertainty, controversy, and trade secrecy. Both theoretical and experimental studies are extremely difficult and expensive. It is probably the most uncontrollable variable in racing today. As such, it is the source of many highs and lows. An improvement in modeling or design, even if it is found by lucky accident, can lead to several years of domination by one tire company, as with BFGoodrich in autocrossing now. An unfortunate choice of tire by a competitor can lead to frustration and a disastrous hole in the budget.

This month, we investigate the physics of tire adhesion a little more deeply than in the past. In Parts 2, 4, and 7, we used the simple friction model given by 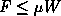, where 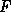is the maximum traction force available from a tire; 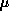, assumed constant, is the coefficient of friction; and 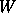is the instantaneous vertical load, or weight, on a tire. While this model is adequate for a rough, intuitive feel for tire behavior, it is grossly inadequate for quantitative use, say, for the computer program we began in Part 8 or for race car engineering and set up.

I am not a tire engineer. As always, I try to give a fresh look at any topic from a physicist's point of view. I may write things that are heretical or even wrong, especially on such a difficult topic as tire mechanics. I invite debate and corrections from those more knowledgeable than I. Such interaction is part of the fun of these articles for me.

I call this month's topic 'grip angle.' The grip angle is a quantity that captures, for many purposes, the complex and subtle mechanics of a tire. Most writers call this quantity 'slip angle.' I think this name is misleading because it suggests that a tire works by slipping and sliding. The truth is more complicated. Near maximum loads, the contact patch is partly gripping and partly slipping. The maximum net force a tire can yield occurs at the threshold where the tire is still gripping but is just about to give way to total slipping. Also, I have some difficulties with the analyses of slip angle in the literature. I will present these difficulties in these articles, unfortunately, probably without resolution. For these reasons, I give the quantity a new name.

A tire is an elastic or deformable body. It delivers forces to the car by stretching, compressing, and twisting. It is thus a very complex sort of spring with several different ways, or modes, of deformation. The hypothetical tire implied by 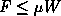with constant 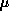would be a non-elastic tire. Anyone who has driven hard tires on ice knows that non-elastic tires are basically uncontrollable, not just because 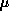is small but because regular tires on ice do not twist appreciably.

The first and most obvious mode of derformation is radial. This deformation is along the radius of the tire, the line from the center to the tread. It is easily visible as a bulge in the sidewall near the contact patch, where the tire touches the ground. Thus, radial compression varies around the circumference.

Second is circumferential deformation. This is most easily visble as wrinkling of the sidewalls of drag tires. These tires are intentionally set up to deform dramatically in the circumferential direction.

Third is axial deformation. This is a deflection that tends to pull the tire off the (non-elastic) wheel or rim.

Last, and most important for cornering, is torsional deformation. This is a difference in axial deflection from the front to the back of the contact patch. Fundamentally, radial, circumferential, and axial deformation furnish a complete description of a tire. But it is very useful to consider the differencesin these deflections around the circumference.

Let us examine exactly how a tire delivers cornering force to the car. We can get a good intuition into the physics with a pencil eraser. Get a block eraser, of the rectangular kind like 'Pink Pearl' or 'Magic Rub.' Stand it up on a table or desk and think of it as a little segment of the circumference of a tire. Think of the part touching the desk as the contact patch. Grab the top of the eraser and think of your hand as the wheel or rim, which is going to push, pull, and twist on the segment of tire circumference as we go along the following analysis.

Consider a car traveling at speed in a straight line. Let us turn the steering wheel slightly to the right (twist the top of the eraser to the right). At the instant we begin turning, the rim (your hand on the eraser), at a circumferential position just behind the contact patch, pushes slightly leftward on the bead of the tire. Just ahead of the contact patch, likewise, the rim pulls the bead a little to the right. The push and pull together are called a force couple. This couple delivers a torsional, clockwise stress to the inner part of the tire carcass, near the bead. This stress is communicated to the contact patch by the elastic material in the sidewalls (or the main body of the eraser). As a result of turning the steering wheel, therefore, the rim twists the contact patch clockwise.

The car is still going straight, just for an instant. How are we going to explain a net rightward force from the road on the contact patch? This net force mustbe there, otherwise the tire and the car would continue in a straight line by Newton's First Law.

Consider the piece of road just under the contact patch at the instant the turn begins. The rubber particles on the left side of the patch are going a little bit faster with respect to the road than the rest of the car and the rubber particles on the right side of the patch are going a little bit slower than the rest of the car. As a result, the left side of the patch grips a little bit less than the right. The rubber particles on the left are more likely to slide and the ones on the right are more likely to grip. Thus, the left edge of the patch 'walks' a little bit upward, resulting in a net clockwise twisting motion of the patch. The torsional stress becomes a torsional motion. As this motion is repeated from one instant to the next, the tire (and the eraser-I hope you are still following along with the eraser) walks continuosly to the right.

The better grip on the right hand side of the contact patch adds up to a net rightward force on the tire, which is transmitted back through the sidewall to the car. The chassis of the car begins to yaw to the right, changing the direction of the rear wheels. A torsional stress on the rear contact patches results, and the rear tires commence a similar 'walking' motion.

The wheel (your hand) is twisted more away from the direction of the car than is the contact patch. The angular difference between the direction the wheel is pointed and the direction the tire walks is the grip angle. All quantities of interest in tire mechanics-forces, friction coefficients, etc., are conventionally expressed as functions of grip angle.

In steady state cornering, as in sweepers, an understeering car has larger grip angles in front, and an oversteering car has larger grip angles in the rear. How to control grip angles statically with wheel alignment and dynamically with four-wheel steering are subjects for later treatment.

The greater the grip angle, the larger the cornering force becomes, up to a point. After this point, greater grip angle delivers less force. This point is analogous to the idealized adhesive limit mentioned earlier in this series. Thus, a real tire behaves qualitativelylike an ideal tire, which grips until the adhesive limit is exceeded and then slides. A real tire, however, grips gradually better as cornering force increases, and then grips gradually worse as the limit is exceeded.

The walking motion of the contact patch is not entirely smooth, or in otherwords, somewhat discrete. Individual blocks of rubber alternately grip and slide at high frequency, thousands of times per second. Under hard cornering, the rubber blocks vibrating on the road make an audible squaling sound. Beyond the adhesive limit, squealing becomes a lower frequency sound, 'squalling,' as the point of optimum efficiency of the walking process is bypassed.

There is a lot more to say on this subject, and I admit that my first attempts at a mathematical analysis of grip angle and contact patch mechanics got bogged down. However, I think we now have an intuitive, conceptual basis for better modeling in the future.

Speaking of the future, summarize briefly the past of and plans for the Physics of Racing series. The following overlapping threads run through it:

Tire Physics: concerns adhesion, grip angle, and elastic modeling. This has been covered in Parts 2, 4, 7, and 10, and will be covered in several later parts.
Car Dynamics: concerns handling, suspension movement, and motion of a car around a course; has been covered in Parts 1, 4, 5, and 8 and will continue.
Drive Line Physics: concerns modeling of engine performance and acceleration. Has been covered in Parts 3, 6, and 9 and will also continue.
Computer Simulation: concerns the design of a working program that captures all the physics. This is the ultimate goal of the series. It was begun in Part 8 and will eventually dominate discussion.

The following is a list of articles that have appeared so far:

Weight Transfer
Keeping Your Tires Stuck to the Ground
Basic Calculations
There is No Such Thing as Centrifugal Force
Introduction to the Racing Line
Speed and Horsepower
The Circle of Traction
Simulating Car Dynamics with a Computer Program
Straights
Grip Angle

and the following is a tentativelist of articles I have planned for the near future (naturally, this list is 'subject to change without notice'):

Springs and Dampers,: presenting a detailed model of suspension movement (suggested by Bob Mosso)
Transients,: presenting the dynamics of entering and leaving corners, chicanes, and slaloms (this one suggested by Karen Babb)
Stability,: explaining why spins and other losses of control occur
Smoothness,: exploring what, exactly, is meant by smoothness
Modeling Car Data: in a computer program; in several articles
Modeling Course Data: in a computer program; also in several articles

In practice, I try to keep the lengths of articles about the same, so if a topic is getting too long (and grip angle definitely did), I break it up in to several articles.

converted by: rck@home.net
Thu Sep 29 14:12:20 PDT 1994

Discuss this article in the forums

Date this article was posted to GameDev.net: 1/7/2002
(Note that this date does not necessarily correspond to the date the article was written)

See Also:
Physics Tutorials