An Introduction To Digital Image Processing
|
|
ADVERTISEMENT |
Disclaimer
This document is to be distributed for free and without any modification from its original contents. The author declines all responsibility in the damage this document or any of the things you will do with it might do to anyone or to anything. This document (and any of its contents) is not copyrighted and is free of all rights, you may thus use it, modify it or destroy it without breaking any international law.
However, there are no warranties or such that the content of the document is error proof. If you found an error please check the latest version of this paper on my homepage before mailing me.
According to the author's will, you may not use this document for commercial profit directly, but you may use indirectly its intellectual contents; in which case I would be pleased to receive a mail of notice or even thanks. The algorithms and methods explained in this article are not totally optimised, they are sometimes simplified for pedagogical purposes and you may find some redundant computations or other voluntary clumsiness. Please be indulgent and self criticise everything you might read. Hopefully, lots of this stuff was taken in sources and books of reference; as for the stuff I did: it has proven some true efficiency in test programs I made and which work as wanted. As said in the introduction: If you have any question or any comment about this text, please send it to the above email address, I'll be happy to answer as soon as possible. Finally, notice that all the source code quoted in this article is available here: http://teachme.free.fr/dsp.zip. You will need the Allegro graphical library and preferably Microsoft Visual C++ 6.0 to compile the project.
Introduction
Digital image processing remains a challenging domain of programming for several reasons. First the issue of digital image processing appeared relatively late in computer history, it had to wait for the arrival of the first graphical operating systems to become a true matter. Secondly, digital image processing requires the most careful optimisations and especially for real time applications. Comparing image processing and audio processing is a good way to fix ideas. Let us consider the necessary memory bandwidth for examining the pixels of a 320x240, 32 bits bitmap, 30 times a second: 10 Mo/sec. Now with the same quality standard, an audio stereo wave real time processing needs 44100 (samples per second) x 2 (bytes per sample per channel) x 2 (channels) = 176Ko/sec, which is 50 times less.
Obviously we will not be able to use the same signal processing techniques in both audio and image. Finally, digital image processing is by definition a two dimensions domain; this somehow complicates things when elaborating digital filters.
We will explore some of the existing methods used to deal with digital images starting by a very basic approach of colour interpretation. As a more advanced level of interpretation comes the matrix convolution and digital filters. Finally, we will have an overview of some applications of image processing.
This guide assumes the reader has a basic signal processing understanding (Convolutions and correlations should sound common places) and also some algorithmic notions (complexity, optimisations). The aim of this document is to give the reader a little overview of the existing techniques in digital image processing. We will neither penetrate deep into theory, nor will we in the coding itself; we will more concentrate on the algorithms themselves, the methods. Anyway, this document should be used as a source of ideas only, and not as a source of code. If you have a question or a comment about this text, please send it to the above email address, I'll be happy to answer as soon as possible. Please enjoy your reading.
I – A simple approach to image processing
1 – The colour data: Vector representation
a - Bitmaps
The original and basic way of representing a digital colored image in a computer's memory is obviously a bitmap. A bitmap is constituted of rows of pixels, contraction of the words 'Picture Element'. Each pixel has a particular value which determines its appearing color. This value is qualified by three numbers giving the decomposition of the color in the three primary colors Red, Green and Blue. Any color visible to human eye can be represented this way. The decomposition of a color in the three primary colors is quantified by a number between 0 and 255. For example, white will be coded as R = 255, G = 255, B = 255; black will be known as (R,G,B) = (0,0,0); and say, bright pink will be : (255,0,255). In other words, an image is an enormous two-dimensional array of color values, pixels, each of them coded on 3 bytes, representing the three primary colors. This allows the image to contain a total of 256x256x256 = 16.8 million different colors. This technique is also know as RGB encoding, and is specifically adapted to human vision. With cameras or other measure instruments we are capable of 'seeing' thousands of other 'colors', in which cases the RGB encoding is inappropriate.
The range of 0-255 was agreed for two good reasons: The first is that the human eye is not sensible enough to make the difference between more than 256 levels of intensity (1/256 = 0.39%) for a color. That is to say, an image presented to a human observer will not be improved by using more than 256 levels of gray (256 shades of gray between black and white). Therefore 256 seems enough quality. The second reason for the value of 255 is obviously that it is convenient for computer storage. Indeed on a byte, which is the computer's memory unit, can be coded up to 256 values.
As opposed to the audio signal which is coded in the time domain, the image signal is coded in a two dimensional spatial domain. The raw image data is much more straight forward and easy to analyse than the temporal domain data of the audio signal. This is why we wiil be able to do lots of stuff and filters for images without tranforming the source data, this would have been totally impossible for audio signal. This first part deals with the simple effects and filters you can compute without transforming the source data, just by analysing the raw image signal as it is.
The standard dimensions, also called resolution, for a bitmap are about 500 rows by 500 columns. This is the resolution encountered in standard analogical television and standard computer applications. You can easily calculate the memory space a bitmap of this size will require. We have 500 x 500 pixels, each coded on three bytes, this makes 750 Ko. It might not seem enormous compared to the standards of hard drives but if you must deal with an image in real time processing things get tougher. Indeed rendering images fluidly demands a minimum of 30 images per second, the required bandwidth of 10 Mo/sec is enormous. We will see later that the limitation of data access and transfer in RAM has a crucial importance in image processing, and sometimes it happens to be much more important than limitation of CPU computing, which may seem quite different from what one can be used to in optimization issues. Notice that, with modern compression techniques such as JPEG 2000, the total size of the image can be easily divided by 50 without losing a lot of quality, but this is another topic.
b – Vector representation of colors
As we have seen, in a bitmap, colors are coded on three bytes representing their decomposition on the three primary colours. It sounds obvious to a mathematician to immediately interpret colors as vectors in a three dimension space where each axis stands for one of the primary colors. Therefore we will benefit of most of the geometric mathematical concepts to deal with our colors, such as norms, scalar product, projection, rotation or distance. This will be really interesting for some kind of filters we will see soon. Figure 1, illustrates this new interpretation:
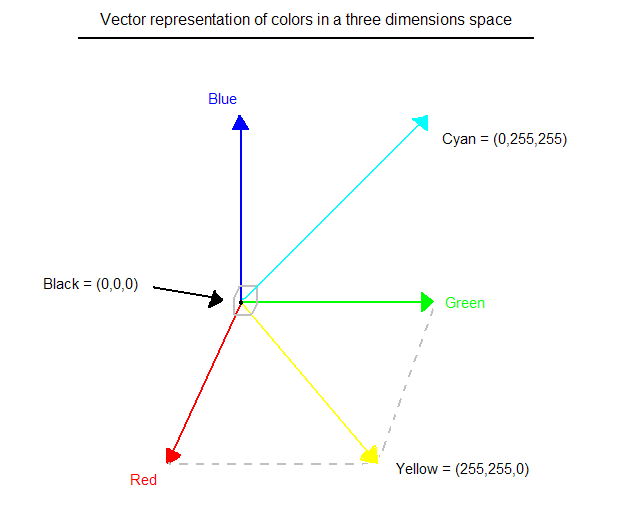
Figure 1 : Vector representation of colors
2 – Immediate application to filters
a – Edge Detection
From what we have said before we can quantify the 'difference' between two colors by computing the geometric distance between the vectors representing those two colors. Lets consider two colors C1 = (R1,G1,B1) and C2 = (R2,B2,G2), the distance between the two colors is given by the formula :
![]()
(R1)
This leads us to our first filter: edge detection. The aim of edge detection is to determine the edge of shapes in a picture and to be able to draw a result bitmap where edges are in white on black background (for example). The idea is very simple; we go through the image pixel by pixel and compare the colour of each pixel to its right neighbour, and to its bottom neighbour. If one of these comparison results in a too big difference the pixel studied is part of an edge and should be turned to white, otherwise it is kept in black. The fact that we compare each pixel with its bottom and right neighbour comes from the fact that images are in two dimensions. Indeed if you imagine an image with only alternative horizontal stripes of red and blue, the algorithms wouldn't see the edges of those stripes if it only compared a pixel to its right neighbour. Thus the two comparisons for each pixel are necessary. So here is the algorithm in symbolic language and in C.
- For every pixel ( i , j ) on the source bitmap
- Extract the (R,G ,B) components of this pixel, its right neighbour (R1,G1,B1), and its bottom neighbour (R2,G2,B2)
- Compute D(C,C1) and D(C,C2) using (R1)
- If D(C,C1) OR D(C,C2) superior to a parameter K, then we have an edge pixel !
Translated in C language using allegro 4.0 (references in the sources) gives:
for(i=0;i<temp->w-1;i++){
for(j=0;j<temp->h-1;j++){
color=getpixel(temp,i,j);
r=getr32(color);
g=getg32(color);
b=getb32(color);
color1=getpixel(temp,i+1,j);
r1=getr32(color1);
g1=getg32(color1);
b1=getb32(color1);
color2=getpixel(temp,i,j+1);
r2=getr32(color2);
g2=getg32(color2);
b2=getb32(color2);
if((sqrt((r-r1)*(r-r1)+(g-g1)*(g-g1)+(b-b1)*(b-b1))>=bb)||
(sqrt((r-r2)*(r-r2)+(g-g2)*(g-g2)+(b-b2)*(b-b2))>=bb)){
putpixel(temp1,i,j,makecol(255,255,255));
}
else{
putpixel(temp1,i,j,makecol(0,0,0));
}
}
}
This algorithm was tested on several source images of different types and it gives fairly good results. It is mainly limited in speed because of frequent memory access. The two square roots can be removed easily by squaring the comparison; however, the colour extractions cannot be improved very easily. If we consider that the longest operations are the getpixel function,get*32 and putpixel functions, we obtain a polynomial complexity of 4*N*M, where N is the number of rows and M the number of columns. This is not reasonably fast enough to be computed in real time. For a 300x300x32 image I get about 26 transforms per second on an Athlon XP 1600+. Quite slow indeed.
Here are the results of the algorithm on an example image:

Picture 1 : Edge detection Results
A few words about the results of this algorithm: Notice that the quality of the results depends on the sharpness of the source image. If the source image is very sharp edged, the result will reach perfection. However if you have a very blurry source you might want to make it pass through a sharpness filter first, which we will study later. Another remark, you can also compare each pixel with its second or third nearest neighbours on the right and on the bottom instead of the nearest neighbours. The edges will be thicker but also more exact depending on the source image's sharpness. Finally we will see later on that there is another way to make edge detection with matrix convolution.
b – Color extraction
The other immediate application of pixel comparison is color extraction. Instead of comparing each pixel with its neighbors, we are going to compare it with a given color C1. This algorithm will try to detect all the objects in the image that are colored with C1. This was quite useful for robotics for example. It enables you to search on streaming images for a particular color. You can then make you robot go get a red ball for example. We will call the reference color, the one we are looking for in the image C0 = (R0,G0,B0).
- For every pixel ( i , j ) on the source bitmap
- Extract the C = (R,G ,B) components of this pixel.
- Compute D(C,C0) using (R1)
- If D(C,C0) inferior to a parameter K, we found a pixel which colour's matches the colour we are looking for. We mark it in white. Otherwise we leave it in black on the output bitmap.
Translated in C language using Allegro 4.0 (references in the sources) gives:
for(i=0;i<temp->w-1;i++){
for(j=0;j<temp->h-1;j++){
color=getpixel(temp,i,j);
r=getr32(color);
g=getg32(color);
b=getb32(color);
if(sqrt((r-r0)*(r-r0)+(g-g0)*(g-g0)+(b-b0)*(b-b0))<=aa){
putpixel(temp1,i,j,makecol(255,255,255));
}
else{
putpixel(temp1,i,j,makecol(0,0,0));
}
}
}
Once again, even if the square root can be easily removed it doesn't really affect the speed of the algorithm. What really slows down the whole loop is the NxM getpixel accesses to memory and the get*32 and putpixel. This determines the complexity of this algorithm: 2xNxM, where N and M are respectively the numbers of rows and columns in the bitmap. The effective speed measured on my computer is about 40 transforms per second on a 300x300x32 source bitmap. Here are the results I obtained using this algorithm searching for whites shape in the source bitmap:
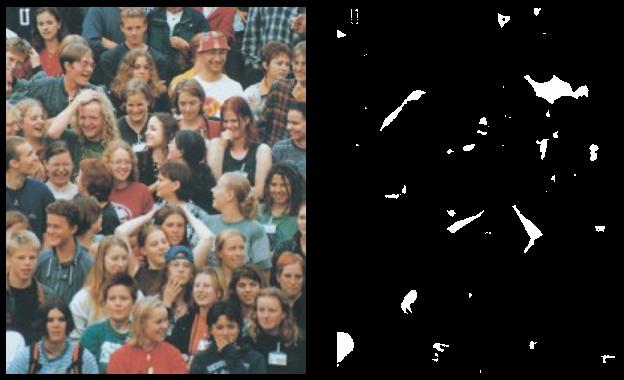
Picture 2 : White Extraction Results
c – Color to grayscale conversion
Regarding the 3D color space, grayscale is symbolized by the straight generated by the (1,1,1) vector. Indeed, the shades of grays have equal components in red, green and blue, thus their decomposition must be (n,n,n), where n is an integer between 0 and 255 (example : (0,0,0) black, (32,32,32) dark gray, (128,128,128) intermediate gray, (192,192,192) bright gray, (255,255,255) white etc…). Now the idea of the algorithm is to find the importance a color has in the direction of the (1,1,1) vector. We will use scalar projection to achieve this. The projection of a color vector C = (R,G,B) on the vector (1,1,1) is computed this way :
![]()
(R2)
![]()
(R3)
However the projection value can reach up to 441.67, which is the norm of the white color (255,255,255). To avoid having numbers above 255 limit we will multiply our projection value by a factor 255/441,67=1/sqrt(3). Thus the formula simplifies a little giving:
![]()
(R4)
So in fact converting a color to a grayscale value is just like taking the average of its red, green and blue components. You can also adapt the (R3) formula to other color-scales. For example you can choose to have a red-scale image, Redscale(C)=R, or a yellow-scale image, Yellowscale(C)=(G+B)/sqrt(6) etc…
- For every pixel ( i , j ) on the source bitmap
- Extract the C = (R,G ,B) components of this pixel.
- Compute Grayscale(C) using (R4)
- Mark pixel ( i , j ) on the output bitmap with color (Grayscale(C), Grayscale(C), Grayscale(C)).
C source code equivalent is :
for(i=0;i<temp->w-1;i++){
for(j=0;j<temp->h-1;j++){
color=getpixel(temp,i,j);
r=getr32(color);
g=getg32(color);
b=getb32(color);
h=(r+b+g)/3;
putpixel(temp1,i,j,makecol(h,h,h));
}
}
It's impossible to optimize this algorithm regarding its simplicity but we can still give its computing complexity which is given by the number of pixel studied: NxM, (N,M) is the resolution of the bitmap. The execution time on my computer is the same as in the previous algorithm, still about 35 transforms per second. Here is the result of the algorithm on a picture:

Picture 3 : Grayscale conversion Results
3 – Grayscale transforms: light and contrast
a – Grayscale transforms
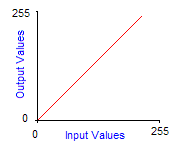
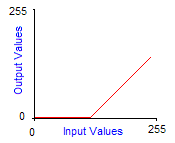
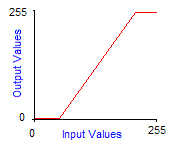
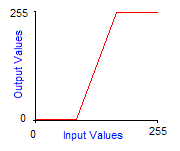
Grayscale transforms are integer functions from [0,255] to [0,255], thus to any integer value between 0 and 255 we make another value between 0 and 255 correspond. To obtain the image of a color by a grayscale transform, it must be applied to the three red, green and blue components separately and then reconstitute the final color. The graph of grayscale transform is called an output look-up table, or gamma-curve. In practice you can control the gamma-curve of your video-card to set lightness or contrast, so that each time it sends a pixel to the screen, it makes it pass through the grayscale transform first. Here are the effects of increasing contrast and lightness to the gamma-curve of the corresponding grayscale transform:
 |
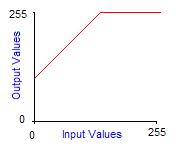 |
| Normal grayscale transform | Increased brightness by 128 |
 |
 |
| Decreased brightness by 128 | Increased contrast by 15° |
 |
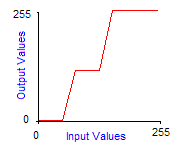 |
| Increased contrast by 30° | Increased contrast by 30° at 64 and 150 |
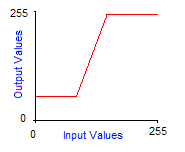 |
|
| Increased brightness and contrast |
Notice that if you want to compose brightness and contrast transforms you should first apply the contrast transform and then the brightness transform. One can also easily create his own grayscale transform to improve the visibility of an image. For example, if you have a very dark image with a small bright zone in it. You cannot increase a lot brightness because the bright zone will saturate quickly but the idea is to increase the contrast exactly where there are the most pixels, in this case: for low values of colors (dark). This will have the effect of flattening the colors histogram and making the image use a wider range of colors, thus making it more visible. So, first the density histogram must be built, counting the number of pixels for each 0-255 value. Then we built the contrast curve we want, finally we integrate to obtain the final transform. The integration comes from the fact that contrast is a slope value, therefore to come back to the contrast transform function we must integrate. Those figures explain this technique:
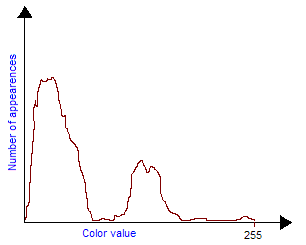 |
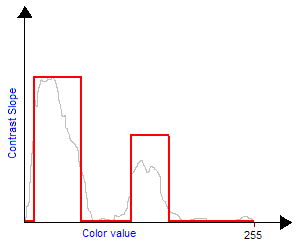 |
| Bitmap input color histogram: two large amounts of pixels in thin color bandwidths. | The contrast slope must be big in those two areas to flatten the input histogram. |
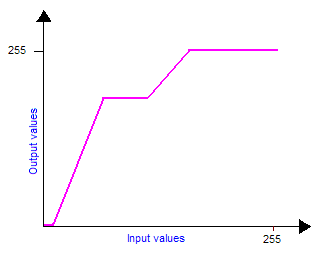 |
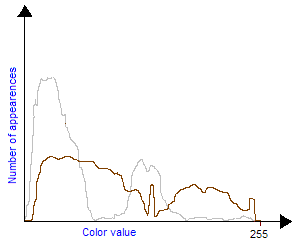 |
| The contrast transform: It is obtained by integrating the previous plot. | The input bitmap color histogram before and after the contrast transform: Now pixels are averagely distributed on the whole color bandwidth. |
b – Light and contrast
Light and contrast transforms are immediate to implement: once the output look-up table is saved into memory once and for all, each pixel is passed trough this table and marked on the output bitmap. The look-up table will be represented simply as a list. The index of the list will stand for the input color value and the contents of the list will be the output. So calling list[153] will give us the image of grayscale level 153 by our transform.
- Generate the look-up table for the desired transform (Light or contrast or any other). For each index j from 0 to 255 is stored its image by the transform in transform_list[ j ].
- For every pixel ( i , j ) on the source bitmap
- Extract the C = (R,G ,B) components of this pixel.
- Mark pixel ( i , j ) on the output bitmap with color (transform_list[R], transform_list[G], transform_list[B]).
In the C source code implementation for contrast, the float variable contrast quantifies the angle of the slope (in radians) of the contrast transform like in figure 2. If contrast is defined as pi/4 there will be no changes in the image, as this corresponds to the 'normal' transform of figure 2. Significant changes start when contrast > pi/4 + 15°. If contrast reaches 0 all the image will be gray because the transform will be a horizontal straight at 128. If contrast becomes very big, any color value becomes either 0 or 255 depending on its position around 128, so the output bitmap will have only the 8 possible colors only made of 255 or 0: (255,255,255), (255,255,0), (255,0,255), (0,255,255), (255,0,0), (0,255,0), (0,0,255), (0,0,0).
for(i=0;i<256;i++){
if(i<(int)(128.0f+128.0f*tan(contrast))&&i>(int)(128.0f-128.0f*tan(contrast)))
Contrast_transform[i]=(i-128)/tan(contrast)+128;
else if(i>=(int)(128.0f+128.0f*tan(contrast)))
Contrast_transform[i]=255;
else
Contrast_transform[i]=0;
}
for(i=0;i<temp->w-1;i++){
for(j=0;j<temp->h-1;j++){
color=getpixel(temp,i,j);
r=getr32(color);
g=getg32(color);
b=getb32(color);
putpixel(temp1,i,j,makecol(Contrast_transform[r],Contrast_transform[g],
Contrast_transform[b]));
}
}
C source code implementation for brightness:
for(i=0;i<256;i++){
Light_transform[i]=i+light;
if(Light_transform[i]>255)
Light_transform[i]=255;
if(Light_transform[i]<0)
Light_transform[i]=0;
}
for(i=0;i<temp->w-1;i++){
for(j=0;j<temp->h-1;j++){
color=getpixel(temp,i,j);
r=getr32(color);
g=getg32(color);
b=getb32(color);
putpixel(temp1,i,j,makecol(Contrast_transform[r],Contrast_transform[g],
Contrast_transform[b]));
}
}
The efficiency of the algorithm is limited by the getpixel and putpixel calls and the speed is the same as the last two algorithms: about 40 transforms per second on my computer. Here are some examples of outputs:

Picture 4 : Brightness transform result
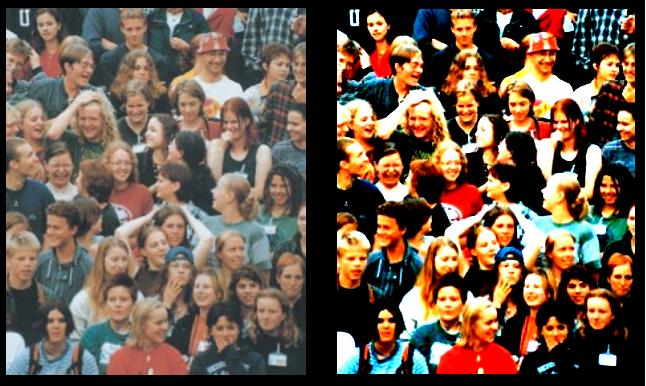
Picture 5 : Contrast transform result
4 – Resizing and rotating algorithms
a – Resizing algorithm
The resizing of an image is far from being trivial. A few techniques exist, each giving more or less good results in stretching or squeezing. Linear resizing is what we will be studying here, I haven't experienced other methods and I won't be able to compare linear resizing with other methods. However, the resizing process is rarely something done for real-time matters. The aim is usually to resize the image once, and if the algorithm takes 5 seconds or 10 ms, it doesn't matter much. For this kind of algorithm quality is put ahead of speed. For the following explanation let E(x) be the integer part of x (E(3.14) = 3) and F(x) the fractional part of x (E(3.14) = 0.14).
We will first see how to stretch or squeeze an image along its width; the process is the same for height and you can cumulate both of them to give the bitmap the desired resolution. Let us consider a row of pixels of the output bitmap of width 'wout'. Let us take a pixel of this row and name his column number xi. To find which color this pixel should be, we are going to convert his column xi to its equivalent column 'ci' in the source bitmap (width = 'win') using the formula:
![]()
![]()
(R5)
Thus pixel in column 'xi' in the output bitmap should be in fact the same color as pixel in column 'ci' in the source bitmap. The problem is that 'ci' is a floating point value and one cannot access floating point pixel numbers (no surprise). However, 'ci' falls in between two integer column numbers E(ci) and E(ci)+1 which can be accessed. You can simply convert 'ci' to its actual integer value: E(ci) and choose the color at pixel E(ci) in the source image. This constitutes the 'nearest neighbour' method. There is another way to solve the problem that has the advantage of giving nicer results at high enlarging ratios: linear interpolation.
In fact, the final color we will choose for pixel 'xi' is not exactly that of pixel 'E(ci)' but a linear interpolation between the color of 'E(ci)' and 'E(ci)'+1 using the fractional part of 'ci'. Thus the final color we will choose for the color of the 'xi' pixel in the output bitmap will be computed by this formula:
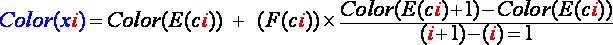
(R6)
Therefore, when stretching the image, the algorithm will try to compensate the lack of information due to the increase of pixels by using linear interpolation. The difference between choosing linear interpolation to compute the color or simply pick the color at 'E(ci)' is not flabbergasting, but the second gives a nice smooth effect and when you have enormous stretches ratio it looks quite nicer than the first one. The first method is more commonly called 'nearest neighbour' and second one is know as 'bi-linear'. Photoshop© uses a third method called 'bi-cubic', but I don't know about it. I used linear interpolation for this screenshot:

Picture 6 : Resizing algorithm result
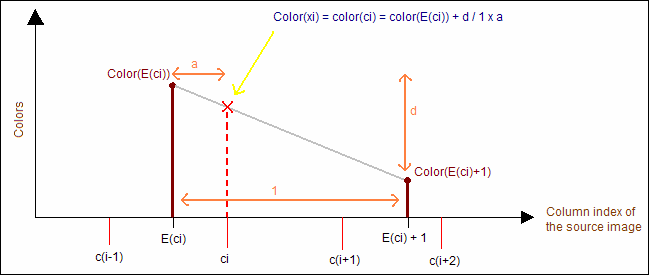
Figure 4: Color interpolation in stretching image
The code in C and the algorithm implementing this resizing methods:
- First we resize the width of the bitmap:
- For every pixel ( i , j ) on the output bitmap
- Compute the ci using formula (R5)
- Extract the (R,G,B) components of pixel E(ci) and E(ci)+1 in source bitmap using (R6)
- Mark pixel ( i , j ) on the output bitmap with color given by formula (R7)
- Repeat the exact same process to resize the height of the bitmap
bs=(float)temp->w/(float)size;
for(i=1;i<size;i++){
for(j=1;j<temp->h-1;j++){
as=(float)i*bs;
es=(int)as;
fs=(int)as+1;
color=getpixel(temp,es,j);
r=getr32(color);
g=getg32(color);
b=getb32(color);
colort=getpixel(temp,fs,j);
rt=getr32(color);
gt=getg32(color);
bt=getb32(color);
cs=modf(as,&gs);
dr=(float)(rt-r);
dg=(float)(gt-g);
db=(float)(bt-b);
putpixel(temp_size,i,j,makecol((int)(r+(float)cs*dr),
(int)(g+(float)cs*dg),(int)(b+(float)cs*db)));
//OR the simple E(ci) method (in which case you can remove lots of stuff above):
//putpixel(temp_size,i,j,makecol((int)r,(int)g,(int)b));
}
}
b – Rotation algorithm
Once again there are different ways of implementing bitmap rotation, the faster they are the more complex they get. We will first study a very basic way and then a much more efficient method. As always there is a little bit of mathematics to understand first. Say x and y are the coordinates of a pixel on the bitmap we can find its image (x',y') by the rotation of center (x0,y0) and of angle α by the following formula:
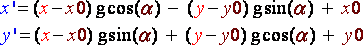
(R8)
If we apply this formula directly, taking each pixel of the source image and passing them through those equations we will obtain lots of holes in the output bitmap. Those wholes are due to the fact that x and y are integers. Necessarily, there will be some x' and y' that will never be reached and which will stay black. The trick is to start from the output image pixels and compute there inverse rotation to find their antecedent by the rotation. Therefore we will use this formula to find (x,y) for every (x',y') of the output bitmap:
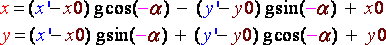
(R9)
Once the antecedent pixel is found, we set the output pixel at the same color. Here is the algorithm and the C source:
- For every pixel (i,j)=(x',y') on the output bitmap
- Compute the antecedent pixel (x,y) of the input image using (R9)
- Mark pixel (i,j) on the output bitmap with the same color as pixel (x,y) of the input bitmap.
cos_val=cos(rangle);
sin_val=sin(rangle);
half_w=temp->w>>1;
half_h=temp->h>>1;
for(j=0;j<temp->h;j++){
for(i=0;i<temp->w;i++){
bs=i-half_w;
cs=j-half_h;
as=bs*sin_val+cs*cos_val+half_w;
gs=bs*cos_val-cs*sin_val+half_h;
color=getpixel(temp,as,gs);
putpixel(temp1,i,j,color);
}
}

Picture 7 : Rotation algorithm result
With this algorithm I have an even better speed than any of the precedent algorithms, about 42 frames per second. The complexity of the algorithm is N*M where N and M are the dimensions of the source bitmap.
There is a way to improve this algorithm. Instead of computing for each pixel of the output bitmap its inverse rotation, we are going to deal with lines. For each horizontal line in the output image, we compute, as we did before, the inverse rotation of its extreme points. Thus we know the color of all the points of this horizontal line because we know all the color of the pixels on the inverse rotation line on the source bitmap. This way we replace lots of rotations calculations (the ones we did for each pixel on the bitmap) by simple linear interpolation with no multiplications. The difference is not that visible on my machine, I gained 3 fps with this algorithm; moreover, if we look at the complexity, it hasn't change. Indeed even with this linear interpolation there is still N*M pixel accesses. It is really the fact that we avoided all the multiplication of the rotations that makes us win 3 fps.
- For every horizontal line in the output bitmap
- Compute the antecedent pixels (x1,y1) and (x2,y2) of the extreme points of the line. (R9)
- For every pixel of line (x1,y1),(x2,y2) on the source image we get its color and set the corresponding pixel on the horizontal line of the output bitmap
cos_val=cos(rangle);
sin_val=sin(rangle);
half_w=temp->w>>1;
half_h=temp->h>>1;
for(j=-1;j<temp->h;j++){
line_count=0;
n=j;
bs=-half_w;
cs=j-half_h;
as=bs*cos_val-cs*sin_val+(half_w);
gs=bs*sin_val+cs*cos_val+(half_h);
r=as;
g=gs;
bs=temp->w-half_w;
cs=j-half_h;
as=bs*cos_val-cs*sin_val+(half_w);
gs=bs*sin_val+cs*cos_val+(half_h);
do_line(temp1,r,g,(int)as,(int)gs,color,Line_make);
if(j==-1)
line_save=line_count;
}
void Line_make(BITMAP* image,int x,int y,int d){
static int lastx=0;
int current_color;
line_count++;
current_color=getpixel(temp,x,y);
if(line_count*temp->w/line_save-lastx>1){
putpixel(temp1,lastx+1,n,current_color);
putpixel(temp1,lastx+2,n,current_color);
}
else{
putpixel(temp1,line_count*
temp->w/line_save,n,current_color);
}
lastx=line_count*temp->w/line_save;
}
4 – Blending
a – Averages
Blending simply consists in averaging the value of two pixels to get a transparency effect, a mix between the two colors. The average can be more or less equilibrated which gives more or less importance to the first or the second pixel. For example if you want to make a blending between two colors C1 and C2 you can use this formula:
![]()
(R10)
Blending is usually done to give transparency effects in 3D games or demos, or transition effects in movies. The blending is often done between two bitmaps, or a bitmap and a color. You can also blend a bitmap with itself, but this results in a sort of blurring which you can achieve much more rapidly with algorithms we will see in the second part of this article. Therefore we will consider we have two bitmaps B1 and B2 we want to blend. They are probably not perfectly edged aligned, and not of the same size. To limit iterations, we copy the biggest bitmap (say B1) on the output bitmap, then we take the smallest bitmap (B2) pixel by pixel, test if the pixel belongs to the other image (B1) at the same time, if it does we average with formula (R10) and set the output pixel, if it doesn't we just set the output pixel directly without changing the color. Anyways once you know that the act of blending is just an averaging, the rest depends on what you want to do.
b – Other blending effects
Blending gives lots of possibilities for cool effects, you can make gradient blending by making the 'α' or 'β' vary; you can have lighting effects, glow effects, transparency effects, water effects, wind effects, lots of the coolest filters in Photoshop© use a simple blending. Once you know this it's rather creativity then technique which makes the difference.

Picture 8 : Blending example
II – Matrix convolution filters
1 – Definition, properties and speed
a – Definition and a bit of theory
Let us first recall a basic principle in signal processing theory: for audio signals for example, when you have a filter (or any kind of linear system) you can compute its response to an entering signal x(t) by convolving x(t) and the response of the filter to a delta impulse: h(t), you then have:
Continuous time:
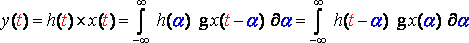
(R11)
Discrete time:
![]()
(R12)
If you are not familiar with this technique and don't want to get bored, you can skip this section which is not crucial to understand the following algorithms. In the same way that we can do for one-dimensional convolution, we can also compute image convolutions, and basically this is what matrix convolution is all about. The difference here is obviously that we are dealing with a two dimensions object: the bitmap. Likewise audio signal, a bitmap can be viewed as a summation of impulses, that is to say scaled and shifted delta functions. If you want to know the output image of a filter, you will simply have to convolve the entering bitmap with the bitmap representing the impulse response of the image filter. The two dimensional delta functions is an image composed by all zeros, except for a single pixel, which has value of one. When this delta function is passed through a linear system, we will obtain a pattern, the impulse response of this system. The impulse response is often called the 'Point spread function' (PSF). Thus convolution matrixes, PSF, filter impulse response or filter kernel represent the same thing. Two dimensional convolution works just like one dimensional discrete convolutions, the output image y of an entering bitmap x, through a filter system of bitmap impulse response h (width and height M) is given by formula:
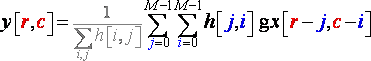
(R13)
Notice that the entering signal (Or the impulse response) alike one dimensional signals must first be flipped left for right and top for bottom before being multiplied and summed: this is explained by the (k-i) index in the sums of (R12); and by the (r-j) and (c-i) indexes in (R13). Most of the time we will deal with symmetrical filters, therefore these flips have no effect and can be ignored; keep in mind that for non symmetrical signals we will need to rotate h before doing anything. By the way two dimensional convolutions is also called matrix convolution.
The presence of a normalising factor in gray in formula (R13), can be explained by the fact that we want y[r,c] to be found between 0 and 255. Therefore we can say that computing y[r,c] is like computing the center of gravity of some x[i,j] color values affected by the weights in the filter matrix. This normalising factor is sometimes included into the filter matrix itself, sometimes you have to add it yourself. Just remember to always check that the numbers possible to obtain with y[r,c] are always between 0 and 255.
Let us have an example of matrix convolution:
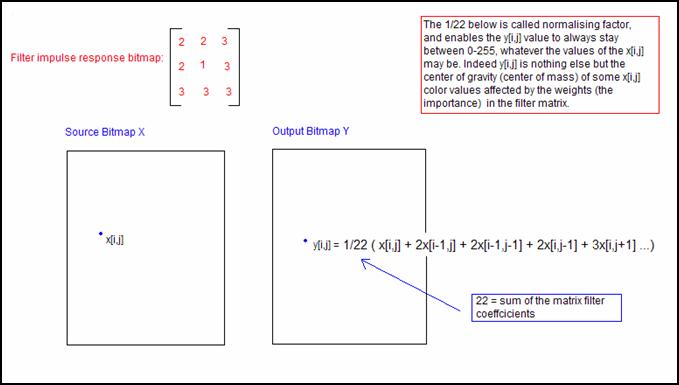
Figure 5: Matrix Convolution
There are numerous types of matrix filters, smoothing, high pass, edge detection, etc… The main issue in matrix convolution is that it requires an astronomic number of computations. For example is a 320x200 image, is convolved with a 9x9 PSF (Pulse spread function), we already need almost six millions of multiplications and additions (320x200x9x9). Several strategies are useful to reduce the execution time when computing matrix convolutions:
- Reducing the size of the filter reduces as much the execution time. Most of the time small filters 3x3 can do the job perfectly.
- Decompose the convolution matrix of the filter into a product of an horizontal vector and a vertical vector: x[r,c] = vert[r] x horz[c]. In which case we can convolve first all the horizontal lines with the horizontal vector and then convolve the vertical line with the vertical vector. Vert[r] and horz[c] are the projections of the matrix on the x and y axis of the bitmap. You can generate an infinity of seperable matrixes filters by choosing a vert[r] and a horz[c] and multiplying them together. This is a really efficient improvement because it brings the global complexity from N²M² to N²M (where N is the number of rows and columns of the input bitmap and M that of the matrix filter).
- Last method is FFT convolution. It becomes really useful for big matrix filters that cannot be reduced. Indeed Convolution in time or space domain is equivalent to multiplying in frequency domain. We will study in detail this method in the last part of this chapter.
1 – A few common filters
a – sharpness filter
Let us have some examples of different filter kernels. The first one will be the sharpness filter. Its aim is to make the image look more precise. The typical matrix convolution for a sharpness filter is:
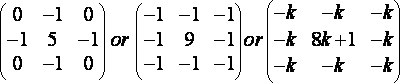
(R14)
Looking at those matrixes you can feel that for each pixel on the source image we are going to compute the differences with its neighbors and make an average between those differences and the original color of the pixel. Therefore this filter will be enhancing the edges. Once you have understood how to compute a matrix convolution the algorithm is easy to implement:
- For every pixel ( i , j ) on the output bitmap
- Compute its color using formula (R13)
- Set the pixel
#define sharp_w 3
#define sharp_h 3
sumr=0;
sumg=0;
sumb=0;
int sharpen_filter[sharp_w][sharp_h]={{0,-1,0},{-1,5,-1},{0,-1,0}};
int sharp_sum=1;
for(i=1;i<temp->w-1;i++){
for(j=1;j<temp->h-1;j++){
for(k=0;k<sharp_w;k++){
for(l=0;l<sharp_h;l++){
color=getpixel(temp,i-((sharp_w-1)>>1)+k,j-
((sharp_h-1)>>1)+l);
r=getr32(color);
g=getg32(color);
b=getb32(color);
sumr+=r*sharpen_filter[k][l];
sumg+=g*sharpen_filter[k][l];
sumb+=b*sharpen_filter[k][l];
}
}
sumr/=sharp_sum;
sumb/=sharp_sum;
sumg/=sharp_sum;
putpixel(temp1,i,j,makecol(sumr,sumg,sumb));
}
}
Unfortunately this filter is not separable and we cannot decompose the filter matrix in the product of a vertical vector and a horizontal vector. The global complexity of the algorithm is N²M² where and N and M are the dimensions of the filter bitmap and of the source bitmap. This algorithm much slower than any of the others we have studied up to now. Use it carefully.

Picture 9: Sharpness filter effects
b – Edge Detection
This algorithm uses matrix convolution to detect edges. I found it much slower than the algorithm seen in the first part for an equivalent result. Here are matrix filters exemples for edge detection:
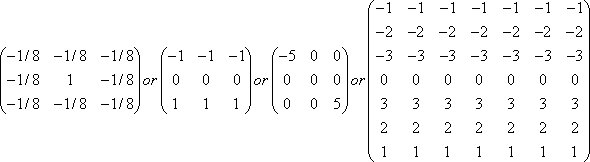
(R15)
The kernel elements should be balanced and arranged to emphasize differences along the direction of the edge to be detected. You may have noticed that some filters emphasize the diagonal edges like the third one, while others stress horizontal edges the fourth and the second. The first is quite efficient because it takes into account edges in any direction. As always, you must choose the filter the most adapted to your problem.
A second important point: notice that the sum of the filter matrix coefficients we usually used as a normalising factor in (R13) is null. Two things to do: we will avoid dividing by zero, we will add to the double sums the value of 128 to bring the color value y[r,c] back into 0-255. The complexity of the algorithm doesn't change N²M².
- For every pixel ( i , j ) on the output bitmap
- Compute its color using formula (R13)
- Set the pixel
#define edge_w 3
#define edge_h 3
sumr=0;
sumg=0;
sumb=0;
int edge_filter[edge_w][edge_h]={{-1,-1,-1},{-1,8,-1},{-1,-1,-1}};
int edge_sum=0; // Beware of the naughty zero
for(i=1;i<temp->w-1;i++){
for(j=1;j<temp->h-1;j++){
for(k=0;k<edge_w;k++){
for(l=0;l<edge_h;l++){
color=getpixel(temp,i-((edge_w-1)>>1)+k,j-((edge_h-1)>>1)+l);
r=getr32(color);
g=getg32(color);
b=getb32(color);
sumr+=r*edge_filter[k][l];
sumg+=g*edge_filter[k][l];
sumb+=b*edge_filter[k][l];
}
}
sumr+=128;
sumb+=128;
sumg+=128;
putpixel(temp1,i,j,makecol(sumr,sumg,sumb));
}
}
c – Embossing filter
The embossing effect gives the optical illusion that some objects of the picture are closer or farther away than the background, making a 3D or embossed effect. This filter is strongly related to the previous one, except that it is not symmetrical, and only along a diagonal. Here are some examples of kernels:
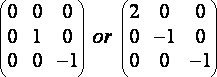
(R16)
Here again we will avoid dividing by the normalising factor 0, and we will add 128 to all the double sums to get correct color values. The implementation of this algorithm is just the same as the prvious one except that you must first convert the image into grayscale.
- Convert the image into grayscale
- For every pixel ( i , j ) on the output bitmap
- Compute its color using formula (R13)
- Set the pixel
#define emboss_w 3
#define emboss_h 3
sumr=0;
sumg=0;
sumb=0;
int emboss_filter[emboss_w][emboss_h]={{2,0,0},{0,-1,0},{0,0,-1}};
int emboss_sum=1;
for(i=1;i<temp->w-1;i++){
for(j=1;j<temp->h-1;j++){
color=getpixel(temp,i,j);
r=getr32(color);
g=getg32(color);
b=getb32(color);
h=(r+g+b)/3;
if(h>255)
h=255;
if(h<0)
h=0;
putpixel(temp1,i,j,makecol(h,h,h));
}
}
for(i=1;i<temp->w-1;i++){
for(j=1;j<temp->h-1;j++){
sumr=0;
for(k=0;k<emboss_w;k++){
for(l=0;l<emboss_h;l++){
color=getpixel(temp1,i-((emboss_w-1)>>1)+k,j-((
emboss_h-1)>>1)+l);
r=getr32(color);
sumr+=r*emboss_filter[k][l];
}
}
sumr/=emboss_sum;
sumr+=128;
if(sumr>255)
sumr=255;
if(sumr<0)
sumr=0;
putpixel(temp2,i,j,makecol(sumr,sumr,sumr));
}
}
Here are the effects of this algorithm:

Picture 9: Embossing filter
d – Gaussian blur filter
As its name suggests, the Gaussian blur filter has a smoothing effect on images. It is in fact a low pass filter. Apart from being circularly symmetric, edges and lines in various directions are treated similarly, the Gaussian blur filters have very advantageous characteristics:
- They are separable into the product of horizontal and vertical vectors.
- Large kernels can be decomposed into the sequential application of small kernels.
- The rows and columns operations can be formulated as finite state machines to produce highly efficient code.
We will only study here the first optimisation, and leave the last two to a further learning (you can find more information on these techniques in the sources of this paper). So, the filter kernel of the Gaussian blur filter is decomposable in the product of a vertical vector and an horizontal vector, here are the possible vectors, multiplied by each other they will produce gaussian blur filters:

Figure 6: Gaussian filters coefficients
(source: An efficient algorithm for gaussian blur filters, by F. Waltz and W. Miller)
Gaussian blur filter kernel example (order 2):
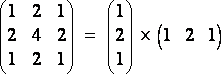
(R17)
What increases greatly the algorithm's speed compared to the previous 'brute force' methods is that we will first convolve rows of the image with the (1 2 1) vector and then the columns of pixels with the (1 2 1)T vector. Thus we will use an intermediary bitmap where will be stored the results of the first convolutions. In the final bitmap will be stored the output of the second stage convolutions. So here is the algorithm with an order 6. The fact that we separated our matrix in a product of vectors, ports the complexity of the algorithm to N²M where M is the size of the filter and N that of the source bitmap. Therefore for a order 6 filter we have 6 times less elementary operations. The result is quite satisfying; on my computer I obtained the equivalent transform rate of the order 3 filters we have seen before. We have thus reached the speed of order 3 filters but with the quality result of an order 6!
- For every pixel ( i , j ) on the intermediate bitmap
- Compute its color using formula (R13), source bitmap pixels and horizontal vector of the matrix decomposition (eg : (1 2 1))
- Set the pixel on the intermediate bitmap
- For every pixel ( i, j ) on the output bitmap
- Compute its color using formula (R13), intermediate bitmap pixels and vertical vector of the matrix decomposition (eg : (1 2 1)T)
- Set the pixel on the output bitmap
#define gauss_width 7
sumr=0;
sumg=0;
sumb=0;
int gauss_fact[gauss_width]={1,6,15,20,15,6,1};
int gauss_sum=64;
for(i=1;i<temp->w-1;i++){
for(j=1;j<temp->h-1;j++){
sumr=0;
sumg=0;
sumb=0;
for(k=0;k<gauss_width;k++){
color=getpixel(temp,i-((gauss_width-1)>>1)+k,j);
r=getr32(color);
g=getg32(color);
b=getb32(color);
sumr+=r*gauss_fact[k];
sumg+=g*gauss_fact[k];
sumb+=b*gauss_fact[k];
}
putpixel(temp1,i,j,makecol(sumr/gauss_sum,sumg/gauss_sum,
sumb/gauss_sum));
}
}
for(i=1;i<temp->w-1;i++){
for(j=1;j<temp->h-1;j++){
sumr=0;
sumg=0;
sumb=0;
for(k=0;k<gauss_width;k++){
color=getpixel(temp1,i,j-((gauss_width-1)>>1)+k);
r=getr32(color);
g=getg32(color);
b=getb32(color);
sumr+=r*gauss_fact[k];
sumg+=g*gauss_fact[k];
sumb+=b*gauss_fact[k];
}
sumr/=gauss_sum;
sumg/=gauss_sum;
sumb/=gauss_sum;
putpixel(temp2,i,j,makecol(sumr,sumg,sumb));
}
}

Picture 10: Gaussian blur filter effects
1 – FFT enhanced convolution
a – FFT with bitmaps
There is a major difference between the use of Fast Fourier Transform in audio signal and in image data. While in the first one fourier analysis was a way to trasform the confusing time domain data into an easy to understand frequency spectrum; the second one converts the straight forward information in spatial domain to a scrambled form in the frequency domain. Therefore, in audio analysis, FFT was a way to 'see' and 'understand' more clearly the signal: now in image processing, FFT messes up the information in an unreadable coding. We will not be able to use FFT in Digital image processing to design filters or to analyse data. Image filters are normally designed in the spatial domain, where the information is encoded in its simplest form. We will always prefer the appelations 'smotthing' and 'shapening' to 'low pass' or 'high pass filter'.
However, some principles of the FFT are still true and very useful in digital image processing: Convolving two functions is equivalent to multiplying in the frequency domain their FFT and then computing an inverse FFT to obtain the resulting signal. The second useful property of the frequency domain is the Fourier Slice Theorem, this therorem deals with the relationship between an image and its projections (the image viewed from its sides. We won't study this theorem here: it would take us far away from our concerns. Let's come back to image convolution using a FFT.
The FFT of an image is very easy to compute once you know how to do one dimensional FFTs (just like in the audio signal). First, if the dimensions of the image are not a power of two we wiil have to increase its size by adding zero pixels; the image must become NxN sized, where N is a power of 2 (32, 64, 128, 256, 1024 …). The two dimensional array that holds the image will be called the real array, and we will use another array of the same dimensions, an imaginary array. To compute the FFT of the image we will take the one-dimensional FFT of each of the rows, followed by the FFT of each of the columns. More precisely, we wiil take the FFT of the N pixel values of row 0 of the real array (original bitmap), store its real part output back into row 0 of real array, and the imaginary part into row 0 of imaginary array. We will repeat this procedure from row 1 to N-1. We will obtain two intermediate images: the real array and the imaginary array. We will then start the process all over again but with columns FFT and using the intermediate images as source. That is to say, compute the FFT of the N pixel values in column 0 of the real array and of the imaginary array (making complex numbers). We will store the result back into column 0 of real and imaginary arrays. After this procedure is repeated through all the columns, we obtain the frequency spectrum of the image, its real part in the real array and its imaginary part in the imaginary array.
Since row and columns are interchangeable in an image, you can start the algorithm by computing FFT on columns followed by rows. The amplitudes of the low frequencies can be found in the corners of the real and imaginary arrays, whereas the high frequencies are close to the center of the output images. The inverse FFT is obviously calculated by taking the inverse FFT of each row and of each column. Properties of the FFT give us a last property of the output images:
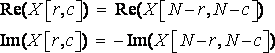
(R18)
The idea of passing to the frequency domain to compute an FFT is the following. We will pass both of the images we want to convolve into the frequency domain, adapting their dimensions so that they have both the same size, NxN power of 2, we will fill empty zones with zeros if necessary. Remember to rotate one of the images to convolve by 180° around its center before starting anything. Indeed convolution, according to its mathematical definition, flips one of the source images. Therefore we will have to compensate it by rotating of of the images first. Once we have the real and imaginary arrays FFT outputs for the two source images, we will multiply each of the real values and imaginary values of one image with each of the real values and imaginary values of the other, this will give us our final image in the frequency domain. Finally we compute the inverse FFT of this final image and we obtain X1 convolved with X2. On the following page you will find in figure 7 the process explained in detail.
The convolution by FFT becomes efficient for big kernels (30x30), and you may notice that its execution time doesn't depend on the kernel's size but on the image's size. Standard convolution's execution time depends on both the kernel size and the source image size. Figure 8 is a graph of the execution time for computing convolutions with different kernel sizes and for two sizes of image (128x128 and 512x512), using FFT, standard floating point convolution (FP) and standard integer convolution (INT).
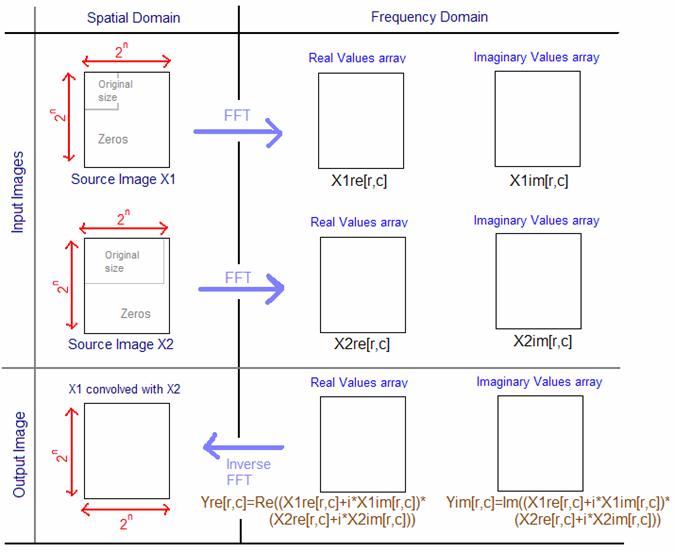
Figure 7: The FFT way of convolving two images
Figure 8: Computing time for different convolution methods and for different kernel sizes
(source: The scientist and engineer's guide to Digital Signal Processing, by Steven W. Smith))
III – Examples of application
1 – Motion Detection and Tracking
a – Static and Dynamic backgrounds
The aim of motion detection is to detect in a streaming video source, which we will consider as a very rapid succession of bitmaps, the presence of moving objects and to be able to track their position. Motion detection in surveillance systems is rarely implemented with software means because it is not trustable enough and good systems remain very expensive, companies usualy prefer hiring surveillance employees. However, video motion detection does exist and works pretty well as long as you know exactly what you want to do. Are you going to have a static background? Is the camera going to move around? Do you want to spot exclusively living entities? Do you know in advance the object which going to move in the camera's field? Lots of questions we will have to answer before making our choices for the algorithm used.
There are two major types of motion detection: static background motion detection and dynamic background motion detection. The first will be used for surveillance means: the surveillance camera doesn't move and has a capture (in a bitmap for example) of the static background it is facing. The second is much more complex. Indeed in the entering streaming video the background moves at the same time as moving objects we want to spot, all the issue consists in seperating the object from the background. Therefore we will make a major hypothesis: the object moves much slower than the background.
b – Static background motion detection
Let us suppose a video camera is facing a static background. The static image of this background, say, when no object is in the field of the camera, is stored in a bitmap. The idea is very simple. When surveillance is turned on, for each frame received (or every n frames, depending on the framerate of the recording system and on the relative speed of the potential target objects) the software compares each pixel of the frame with those of the static background image. If a pixel is very different it is marked as white, if not it is left in black. We will calculate the 'difference' between these two pixels by calculating the distance between them with (R1), and comparing it to a threshold value. Some techniques set this threshold value according to the number of color the arriving frame contains, I haven't tested this technique personally but it seems fairly wise. Therefore after this stage, the suspected moving objects are marked in white pixels, while the background is all set to black. Unfortunately, lights reflections, hardware imperfections, other unpredictable factors, will introduce some parasitical white pixels which don't correspond to real objects moving. We will try to remove those isolated white pixels to purify the obtained image.
Thus we will pass the resulting black and white image through an aliasing filter, which is meant to remove noise. This filter will remove all the isolated noisy white pixels and leave, if there are, the big white zones corresponding to moving objects. Basically we scan the image with a window of NxN pixels (depends on the size of the frames), if the center of the pixel of the NxN square is white, and less than K pixels in the window are set to white then it is set back to black because it is probably just an isolated noise not corresponding to a concrete object moving. Oppositly if more than K pixels are set to white and the center pixel is white we leave it as it is. However, this requires a lot of pixel scanning N²M², where M is the dimension of the frames; therefore we will rather scan the image by squares of NxN, for each of them count the number of white pixels they contain, if it superior to the treshhold value the whole NxN square is set to white on the bitmap else we set it black, we then jumps to the next NxN square. With this technique we limit the pixels access to M² which is a lot better. The output image will seem very squary but this is not a problem.
At that point we should have a black image with perhaps some white zones corresponding to moving objects in the fields of the camera. Thus we can already answer to the basic question: is there a moving object in the camera's field? A simple test on the presence of white pixels on the image will answer. Here is an example stage by stage of the processing:

Picture 10: The static background image of the camera's field

Picture 11: My dog (yes, the weird shape in black) has jumped on the bed to look if there isn't something to eat in the red bag

Picture 12: After comparing each pixel of the current frame with the static background we already have a good idea of the moving shape. Notice all the noise (small isolated pixels in white) due to the poor quality of my webcam. The fact that my dog is searching in the bag makes it move a little, which is also detected on the right of the image.

Picture 13: The aliasing filter has removed all the noise and parasites. We finally isolated the moving shape and we are now capable of giving its exact position, width, height etc…
c – Unknown background (dynamic) motion detection
The case of unknown background motion detection is pretty similar to the previous situation. This becomes useful when you cannot predict the background of the camera's field and therefore cannot apply the previous algorithm. Notice that we will not study here, the motion detection algorithms in which the camera is moving permanently. Here the camera doesn't actually move, nor does it use a background reference like just before. Instead of comparing each received frame to a reference static background we are going to compare the frames received together. This technique is known as frame differentiating.
This is how the algorithm works on a streaming source of frames coming from a video camera: We will store a received frame in bitmap A, wait for the next n frames to pass without doing anything, capture the n+1 frame, compare it to A, store the n+1 frame in A, wait for n frames to pass, capture the 2n+2 frame, compare to A, store in A, and so on. Therefore we will regularly compare two frames together, seperated by n other frames that we will simply loose. This n value, the comparison rate, must be low enough not to miss some moving objects which would go right through the camera's field, but it also must be high enough to see differences between frames if a very slow object is moving in the camera's field. For the example of my webcam and my dog, I took n=10, with a streaming frame rate of 30 fps, this corresponds to 1/3 secs.
When we compare the two frames together we use the same method as seen above, if a pixel changes a lot of color from one frame to another we set it as white, else we leave it in black. We then make the resulting image pass through an aliasing filter and finally we are able to spot the moving objects.
Obviously this technique is less precise than the previous one because we don't spot directly the moving object in itself but we detect the changing zones in the frames and assimilate those changing zones to a part of background which has been recovered recently by a part of the object. Therefore we will only see edges of moving objects. Here is an example of results:

Picture 14: One of the frames we are going to compare (bitmapA)

Picture 15: The second frame to compare, we have skipped 10 frames ever since we saved bitmapA. Therefore the dog has had the time to move and we will see a difference between the frames.

Picture 15: The algorithm sees the zones which have changed colors: corresponding to the head of the dog walking and to my hand I was agitating.

Picture 16: After the aliasing filter only the main zones are left and enable us to situate roughly the moving objects on the camera's field.
1 – Shape recognition
a – Shape recognition by convolution
The aim of shape recognition is to make the computer recognize particular shapes or patterns in a big source bitmap. Like the audio signal with speech recognition, this is far from beeing a trivial issue. Lots of powerful but also very complex methods exist to recognize shapes in an image. The one we are going to study here is very basic and makes a number of assumptions to work correctly. The shape we are going to try to situate on a source image must not be rotated nor distorted on this actual image. This limits a lot the use of this algorithm because in real situations the pattern you search in an image is always a bit rotated or distorted. In one dimensional signal correlation between two signals quantifies how similar they are; in two dimensions the principle is the same. Computing the correlation of the source image and the pattern we are looking for while give us an output image with a peak of white corresponding to the position of the pattern in the image. In fact we make our source image pass through a filter which kernel is the pattern we are looking for. When computing the output image pixel by pixel at one point the kernel and the position of the searched pattern in the image will correspond perfectly, this will give us a peak of white we will be able to situate.
Therefore the implementation of the algorithm is very simple; we compute the matrix convolution of the source image with the kernel, constituted of the pattern we want to search. In this case you will almost be forced to use the FFT convolution, indeed the searched patterns are often more then 30 pixels large, and for kernels of over 30x30 it's faster to use an FFT rather than straight convolution. I tried this algorithm without the FFT optimization and it is very very slow: about one transform per minute!
However the results themselves are quite remarkable, the position of the pattern is well recognized, sometimes with a bit of noise though. A nice way to enhance the results and make the peaks even more precise is to make the kernel pass through an edge enhancement filter; this will make the kernel more selective and precise. Here are the results of the algorithm:

Picture 17: Our source image: will you find the ball before the computer does?

Picture 18: The pattern the algorithm will be looking for.

Picture 19: The white peak corresponding to the ball's position.

Picture 20: Another source image.
![]()
Picture 21: The pattern the algorithm will be looking for.

Picture 22: The white peak corresponds to the positions of the patterns.
Conclusion
Digital image processing is far from being a simple transpose of audio signal principles to a two dimensions space. Image signal has its particular properties, and therefore we have to deal with it in a specific way. The Fast Fourier Transform, for example, which was such a practical tool in audio processing, becomes useless in image processing. Oppositely, digital filters are easier to create directly, without any signal transforms, in image processing.
Digital image processing has become a vast domain of modern signal technologies. Its applications pass far beyond simple aesthetical considerations, and they include medical imagery, television and multimedia signals, security, portable digital devices, video compression, and even digital movies. We have been flying over some elementary notions in image processing but there is yet a lot more to explore. If you are beginning in this topic, I hope this paper will have given you the taste and the motivation to carry on.
Sources and Links
- The Scientist and Engineer's Guide to Digital Image Processing, by Steven W. Smith
- An efficient algorithm for gaussian blur using finite state machines, by F. Waltz and J.Miller
- http://www.catenary.com/
- http://manual.gimp.org/manual/GUM/Plugin_generic.html
- Practical Algorithms for Image Analysis, by M.Seul, L.O'Gorman, M. Sammon
- Digital Image Processing, by R.Gonzalez and R.Woods
- The Pocket Handbook of Imaging Processing Algorithms in C, by H.Myler and A.Weeks
Appendix A : Last minute adds
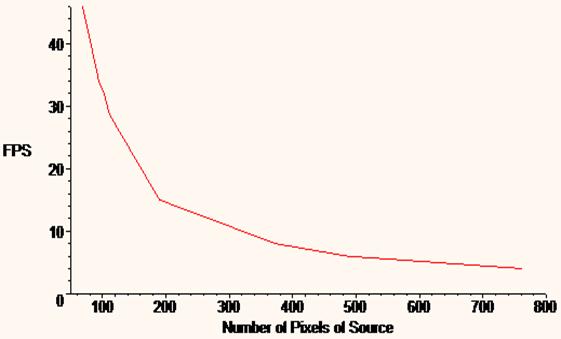
Figure 9: Plot of the Tranforms per second with the color extraction algorithm according to the number of pixels of the source bitmap (/1000). It is fair to conclude that the fps decrease in an hyperbolic way with the number of pixels in the source bitmap. Notice also that it doesn't have anything to do with the complexity of the algorithm which is a straight according to the number of pixels (a*N²).
Discuss this article in the forums
Date this article was posted to GameDev.net: 10/20/2003
(Note that this date does not necessarily correspond to the date the article was written)
See Also:
Featured Articles
General
© 1999-2011 Gamedev.net. All rights reserved. Terms of Use Privacy Policy
Comments? Questions? Feedback? Click here!