sponsors gamedev.net search:

A Math-Magic Relationship In our triangle data structure we have an array of points (p[3]), children (child[4]) and edges (e[3]). Because the triangles are equilateral, there's no guarantee of the orientation of a neighbour relative to t. Rather than trying to track the orientations of all the triangles as down, up-left, up-right etc, and derive specific cases for the interactions between them based on that (which you need to do if you had ordered the points,children, and edges left to right), our counter-clock spiral ordering gives us a unique and simple relationship, though its not immediatly obvious. int j=i+1; if(j>2) j=0; This relationship, with a point, edge, or child index into the appropriate array plugged into i, and the result j, gives us some noteworthy results. If i is an edge, i and j are the appropriate points making that edge. If i is a edge, i and j are the appropriate children along that edge, and i is the edge each child shares with its parent. If i is a point, j is the counter clock-wise point. Splitting Triangles void cLoDManager::Split( cLoDTri* t ); Firstly, Split() being a recursive function, we need to return without action if t is null. It's faster than checking in the calling function the state of t. Then we go through the edge pointers of t. Any edges that are set to NULL indicate a triangle off that edge that is larger than us. Think about this for a moment, if there is a triangle next to us with children, our edge pointer will point to their parent. If it is the same as us, we will also be pointing to a neighboring tri. The only case where no neighbour exists is if we are higher detail than it. Seen as we have a rule, the same rule that ensures this relationship, we Split t->e[n] before we can split ourselves, ensuring that triangles remain within one order of detail of their neighbors. That done, we create three new points, each along the midpoint of our edges. dVector n[3]; n[0] = t->p[0].vMidpoint(t->p[1]); n[1] = t->p[1].vMidpoint(t->p[2]); n[2] = t->p[0].vMidpoint(t->p[2]); These midpoints are what we will use to make our 4 child triangles. These midpoints are the sum of the two points / 2. Note this means even with our four children the mesh of four triangles is flat. We need to normalize each midpoint and multiply it by the radius of the sphere. This provides the spherical displacement. But we can't do that yet. If we do we get the following nasty result. 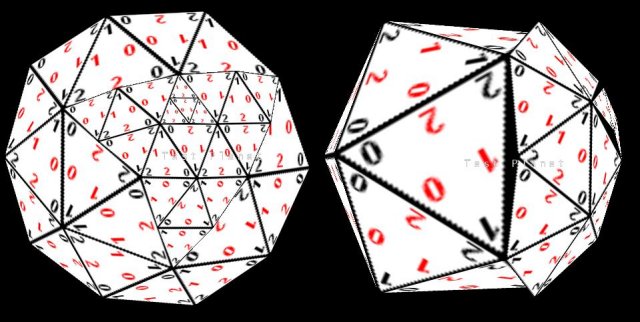There are a few ways to close these gaps. Most of them are very inefficient. The methods I've seen used, eg in Diamond Roam, are to bridge our now larger neighbors points with our displaced midpoint in as few a tessellations as possible. There are 3*2 permutations of this bridging, and it requires excessive management to cope with. Somewhere to keep the hybrid split tris and/or more heinously, determining them during the rendering cycle. It's this that puts people off equ-lods :p Although this method is achievable a little easier with the Magic-Relationship as (ok, really it's with the counter-clock spiral ordering) we remove triangle orientation complications (only 2 permutations of the bridging remain), there's a much simpler and faster solution. Don't fill gaps...

Contents   Data Structure   A Math-Magic Relationship   Don't fill gaps...   The Big Picture   Printable version   Discuss this article The Series   Structure