sponsors gamedev.net search:

"From up here, I can see the big picture" Combining triangles is the opposite of splitting them. Our mesh simplifies back, though in the case of a planet you probably don't want it to simplify back to the original polytope. Thats a discussion for the next article though. Combining is fortunately, very straight-forward (if you got this far). Fundamentally you just delete the children, and remove the parent from the parent list and put it back in the mesh. Like splitting a triangle, theres some bookkeeping to do with the edges and displacements again, but its much more trivial. Also, Combines are not iterative like Splits. Only the triangle we're looking at is operated upon. They must also be parents or there's nothing to combine. We can only combine a triangle if it has children, but no grandkids. You'd think looking at a diagram that there was more involved, like neighbors with grandchildren, but you'll easily note that a neighbour with grandchildren adjacent to any of our edges means we must also be at that level of detail, ie. We wouldn't be here trying to combine this triangle, we'd be further down the sibling list trying to combine one. Trust me, it works. //if t has no children return immediately, no merge if(!t->bHasChildren()) return; //if t has grandchildren, return, cant merge for(int i=0; i<4; i++) if(t->child[i]->bHasChildren()) return; The rest is nothing you haven't seen yet but in reverse. The only noteworthy point here you might forget is that you have to tell neighboring displacements that they must be flat again, or you'll see a gap. Again the spiral counter-clock winding saves us massive switch() case by case algorithmic orientation checks. //we got this far we can do the combine for(int i=0; i<3; i++) { //any neighbors with children, inform them our children //are gone (point them to null) if(t->e[i]->bHasChildren()) { int iEdge=t->e[i]->iSharesEdge(t); if(iEdge!=-1) { int j=iEdge+1; if(j>2)j=0; t->e[i]->child[iEdge]->e[iEdge]=NULL; t->e[i]->child[j]->e[iEdge]=NULL; //correct neighbour child's points dVector n = t->e[i]->child[iEdge]->p[iEdge].vMidpoint(t->e[i]->child[j]->p[j]); int l=j+1; if(l>2)l=0; t->e[i]->child[iEdge]->p[j] = n; t->e[i]->child[j]->p[iEdge] = n; t->e[i]->child[3]->p[l] = n; } } } //delete our children for(int i=0; i<4; i++) { delete t->child[i]; t->child[i]=NULL; } //put triangle back into the mesh t->Remove(); m_llMesh.AddHead(t); Needing something to tessellate? We need a surface to tessellate, a starting structure of equilateral triangles (it works without equilateral triangles but the distortion isn't pretty). In this case, Planets, we will start with an Icosahedron. There is a lower order polytope that would do, the ecohedron, but if you think about an ecohedron for a moment (two pyramids glued together), they have no equator, only poles. The triangles about the poles are manifold, in that the four triangles that make up each 'hemisphere' are initially anchored together at a shared polar point. This creates an unwelcome distortion in the tessellated mesh. As an aside for a moment, as you will see the mesh deals automagically with NULL edge pointers, so this will happily tessellate any open or closed mesh. Its very handy in that respect for planetary ring systems, sheet nebulae etc. I hard code this initial shape into the cLoDManager class. Its fairly straight forward so I'll just reproduce it here without much further explanation. The only change to this is if you were to index this mesh. I haven't done for clarity, though in my own implementations for Entropy I do it for the rendering performance. It also mildly optimizes the Split function. void cLoDManager::BuildPlatonicPolytope() { /* 20 equilaterals (icosahedron) http://astronomy.swin.edu.au/~pbourke/polyhedra/platonic/index.html */ helper_tex.LoadUTGA("textures/orient.tga",false); radius=10; double a,b,phi; phi=(1+sqrtf(5))/2; a = 0.5; b = 1 / (2 * phi); dVector p[60]; p[0]=dVector(0, b, -a); p[1]=dVector(b, a, 0); p[2]=dVector(-b, a, 0); p[3]=dVector(0, b, a); p[4]=dVector(-b, a, 0); p[5]=dVector(b, a, 0); p[6]=dVector(0, b, a); p[7]=dVector(0, -b, a); p[8]=dVector(-a, 0, b); p[9]=dVector(0, b, a); p[10]=dVector(a, 0, b); p[11]=dVector(0, -b, a); p[12]=dVector(0, b, -a); p[13]=dVector(0,-b, -a); p[14]=dVector(a, 0, -b); p[15]=dVector(0, b, -a); p[16]=dVector(-a, 0,-b); p[17]=dVector(0, -b,-a); p[18]=dVector(0, -b, a); p[19]=dVector(b,-a, 0); p[20]=dVector(-b,-a, 0); p[21]=dVector(0, -b,-a); p[22]=dVector(-b,-a, 0); p[23]=dVector(b,-a, 0); p[24]=dVector(-b, a, 0); p[25]=dVector(-a, 0, b); p[26]=dVector(-a, 0, -b); p[27]=dVector(-b,-a, 0); p[28]=dVector(-a, 0,-b); p[29]=dVector(-a, 0, b); p[30]=dVector(b, a, 0); p[31]=dVector(a, 0,-b); p[32]=dVector(a, 0, b); p[33]=dVector(b, -a,0); p[34]=dVector(a, 0, b); p[35]=dVector(a, 0,-b); p[36]=dVector(0, b, a); p[37]=dVector(-a, 0, b); p[38]=dVector(-b, a, 0); p[39]=dVector(0, b, a); p[40]=dVector(b, a, 0); p[41]=dVector(a, 0, b); p[42]=dVector(0, b,-a); p[43]=dVector(-b, a, 0); p[44]=dVector(-a, 0,-b); p[45]=dVector(0, b,-a); p[46]=dVector(a, 0,-b); p[47]=dVector(b, a, 0); p[48]=dVector(0, -b,-a); p[49]=dVector(-a, 0,-b); p[50]=dVector(-b,-a, 0); p[51]=dVector(0, -b,-a); p[52]=dVector(b,-a, 0); p[53]=dVector(a, 0,-b); p[54]=dVector(0, -b, a); p[55]=dVector(-b,-a, 0); p[56]=dVector(-a, 0, b); p[57]=dVector(0, -b, a); p[58]=dVector(a, 0, b); p[59]=dVector(b,-a, 0); for(int k=0; k<60; k++) { p[k].vNormalize(); p[k]*=radius; } cLoDTri* t[20]; int j=0; for(int k=0; k<20; k++) { t[k] = new cLoDTri(p[j],p[j+2],p[j+1]); j+=3; m_llMesh.AddHead(t[k]); } /*build initial neighbour pointers iteratively. Only needs done at lowest lod, subsequently split~combine algorithm does it automatically and quickly (this is slow for higher lod, but fast enough for this primitive)*/ for(cLoDTri* tl = m_llMesh.GetHead(); tl->InList(); tl = tl->GetNext()) for(cLoDTri* tn = m_llMesh.GetHead(); tn->InList(); tn = tn->GetNext()) if(tl!=tn) { for(int i=0; i<3; i++) { int j=((i+1)>2)?0:(i+1); if(tn->SharesPoint(tl->p[i]) && tn->SharesPoint(tl->p[j])) { tl->e[i]=tn; } } } } Conclusion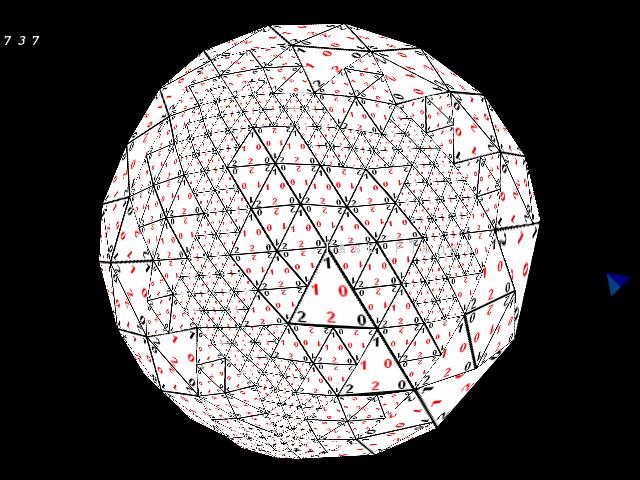 Below is an executable that you can play around with to see the mesh in action. It's not a fully scaled planet, more like an interactive diagram. It makes the structure and tessellation method very plain to see. Requires OpenGL, Win32. Right mouse button rotates you around the lod, mousewheel zooms you in and out. Download(139kb) My Homepage

Contents   Data Structure   A Math-Magic Relationship   Don't fill gaps...   The Big Picture   Printable version   Discuss this article The Series   Structure