Automatic Portal Generation
Introduction
Recently my friend and I have been working on our first 3D game engine. After evaluating several methods, we decided to implement portal-based scene graph management. There are many articles talking about portal-based rendering, but I've rarely see one that mentions how to generate portals automatically in a map editor. The exception is one article called "Binary Space Partioning Trees and Polygon Removal in Real Time 3D Rendering" by Samuel Ranta-Eskola at www.gamedev.net. However when my friend tried to implement the algorithm in the article for our map editor, we found fatal errors in the algorithm, such as unreasonable recursive calls. So we had to design a new algorithm by ourselves. At first we thought it would be very difficult, but after a week's effort, we finally made it, though the algorithm is not perfect. In some cases it will generate a few redundant portals, but it is easy to eliminate those by hand.
If you are trying to implement a portal-based engine,and you do not want to generate the portals by hand (and who would?) keep on reading.
Problem consideration
We export triangle data from 3dsmax to our engine's map editor, so we do not need to develop a CSG map editor like Quake. The task of our map editor is to first generate a BSP tree from the triangle soup we've exported from 3dsmax and then generate portals for each leaf in the BSP tree. There are several points you need to notice in our algorithm:
1. Portals only exist on the plane of the BSP node. This is obvious but very important, because without this assumption, we could not set up this algorithm. We generate a large enough rectangle (exceeding the boundary of the bounding box of the environment) at each non-leaf node, and clip it against other planes (plane of the node and triangles in the leaf) when we traverse down the tree. So finally we have a lot of polygons and portals, and the remaining process is to identify which are real portal and which are not. Actually, we analyse the validity of each portal each time we clip the portal. The rules are as follows (each portal has an attribute bCulled with an initial value of TRUE):
- If a portal is spanning the dividing plane at a node (not a leaf), we clip the portal into 2 portals and set their bCulled flag to be the same as the original one.
- If a portal is divided by a triangle in the leaf, we set the bCulled attribute of the portal on the positive side of the triangle's plane to FALSE, and the negative one to TRUE.
- Finally, after dividing against all triangles, portals with their bCulled attribute set to FALSE are the ones we really want. We can do this because the direction the triangle is facing tells us whether the space is solid or non-solid, and we don't want those portals in solid space.
2. We do not require that the triangles in a leaf form a convex region, which means the portals between regions (a region is a leaf in the bsp tree) can form a concave polygon - which is not suitable for portal rendering. So our algorithm will make sure that all portals generated form a convex polygon, which means that if a portal turns out to be concave, we will generate several convex ones from it. This may appear inefficient, but it comes up infrequently enough that it doesn't present a problem.
3. In order to generate correct portals, we need to assure that the triangle soup forms a closed space and that there is no self intersection (otherwise it will cause some redundant portals). The artists on our team found that making sure the space is closed is relatively easy, but eliminating self intersection isn't. So, we decided to not force artists to meet these requirements in their modelling. Instead, we use some rules to eliminate some obvious redundant portals automatically once the generation process is done. If unreasonable portals remain, it's easy to eliminate them by hand. Fortunately, while implementing the collision detection system, we invented an algorithm that indentifies situations where self-intersetion occurs, so if you use this algorithm to scan the triangle soup and do some subdivision you can eliminate these situations! I will cover this algorithm in a future article.
What's more, we will also generate several convex polygons which can be replaced by one convex polygon during the process, so at later stage we'll also add a process of portal merging.
4.Floating point precision is a problem that you have to handle carefully in the algorithm. At first we generated many obvious redundant portals due to floating point precision errors, but we were able to solve this problem by carefully controlling the tolerance in various situations.
Primary data structures
class CPortal
{
public:
//If the portal's polygon seems like a line segament,it is not reasonable
//this is some kind of tolerance control.
BOOL Reasonable();
Cpolygon m_Polygon;
BOOL m_bCulled;
int m_iLeftNode;
int m_iRightNode;
}
class CSurperPlane
{
public:
void Remove(CPortal *pPortal);
void Add(CPortal *pPortal);
TList<CPortal*> m_LisOfPortals;
}
class CBspNode
{
public:
int m_iTag; //if m_iTag>=0 it is a node else it is a leaf
CPlane m_DividingPlane;
CBspNode *m_pParent;
CBspNode *m_pLeftNode;
CBspNode *m_pRightNode;
Tlist<CTriangle> m_ListOfTriangle;
}
class CBspTree
{
public:
//This is the main algorithm function
void GeneratePortal(CBspTreeNode *pBspNode_, CSuperPlane *pSuperPlane_);
//Test if the triangle is intersecting with the polygon,
//this function needs careful tolerance control
BOOL TriangleIntersectPolygon(CTriangle& Tri_,CPolygon& Polygon_);
//Check the relationship between the plane and the polygon
//polygon on positive side of the plane
// on negative side
// spanning
// coincide
//this function needs a little tolerance control
int CalculateSide(CPlane plane_,CPolygon *pPolygon_);
//use the plane to clip the portal and put the output the data into leftportal
//and rightportal, left means on the positive side of the plane and right means
//on the negative side
void ClipPortal(CPlane plane_, CPortoal *pPortal_,
CPortoal& PortalLeft_, CPortoal& PortalRight_);
CBspNode *m_pRoot;
TList<CSuperPlane*> m_ListOfSuperPlanes;
}
Algorithm pseudocode
Because the algorithm is a bit long, I will give you a simple version first. Note that you must generate a bsp tree before using this algorithm.
void CBspTree::GeneratePortal(CBspTreeNode *pBspNode_, CSuperPlane *pSuperPlane_)
{
if (pBspNode_->IsLeaf ())
{
Use each triangle in pBspNode_ to clip against each portal in pSuperPlane_;
Update validation information of each portal;
Delete those culled portals which connects pBspNode_ in pSuperPlane_;
}
else
{
if (pSuperPlane_)
{
Use dividing plane at pBspNode_ to clip against each portal in pSuperPlane_;
Update connection information of each portal;
GeneratePortal(pBspNode_->m_pLeftNode,pSuperPlane_);
GeneratePortal(pBspNode_->m_pRightNode,pSuperPlane_);
}
if (we have not generated a Super plane at pBspNode_)
{
Create pNewSuperPlane on the dividing plane of pBspNode_
Generate a large portal on pNewSuperPlane;
Clip portal on pNewSuperPlane to make sure it is within the space of pBspNode_
GeneratePortal(pBspNode_->m_pLeftNode,pNewSuperPlane);
GeneratePortal(pBspNode_->m_pRightNode,pNewSuperPlane);
}
}
}
A very simple example
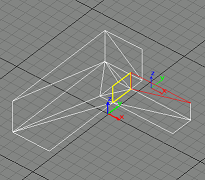
This is a 2 room scene. The BSP Tree has 3 nodes (2 of them are leaves).
Red triangles are those we are using to clip against portals.
Blue polygons indicatate portals that have beel culled (m_bCulled = TRUE)
Yellow polygons indicate portals that have not been culled (m_bCulled = FALSE)
 |
 |
 |
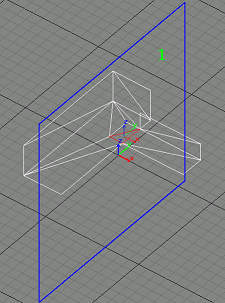Step 1
GeneratePortal(BspNode0,NULL)
We generate a SuperPlane at the dividing plane of the root node of the bsp tree, and we also create a large portal (portal 1) on the SuperPlane(the blue rectangle).
Assume the portal's plane normal points to BspNode0(the left space), and
portal1.m_iLeftNode = -1;
portal1.m_iRightNode = -2;
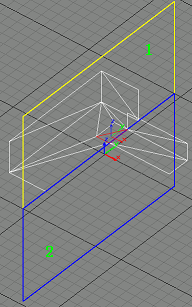
Step 2
GeneratePortal(BspNode1,SuperPlane)
This is a leaf node, so we have to use all the triangles in BspNode1 to clip against all the portals in SuperPlane. We find the first suitable triangle (the red one), and divide portal 1 into portal 1 and portal2. Portal 1 is on the positive side of the triangle, so its m_bCulled member is set to FALSE (and it is shown in yellow). Portal 2 is on the negative side of the triangle, so its m_bCulled member is set to TRUE (and it is shown in blue).
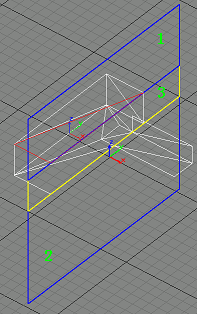
Step3
We find the second suitable triangle, and divide portal 1 into portal 1 and portal 3. Portal 3 is the yellow one and portal 1 is the blue one at the top.
 |
 |
 |
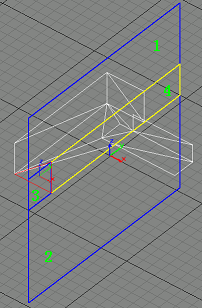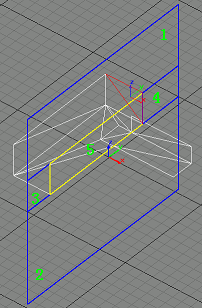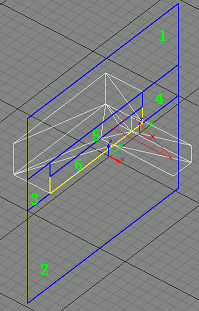Step 4
Next we find the third suitable triangle, and divide portal 3 into portal 3 and portal 4.
Step5
Next we find the last suitable triangle in BspNode1, and clip portal 4 into portal 4 and portal 5.
Note that these pictures are from an old version, where we're doing all portal filter processing in the final step, but actually you can do some filter processing as we describe in the algorithm)
 |
 |
 |
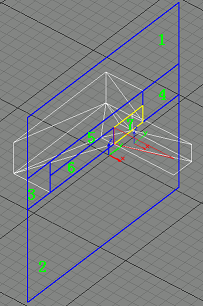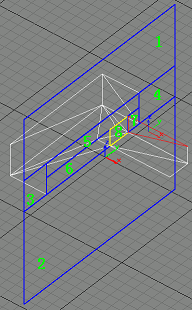Step 6
GeneratePortal(BspNode2,SuperPlane)
BspNode2 is also a leaf node, so we have to use all triangles in the leaf to clip against all the portals in SuperPlane
We find the first suitable trianle in BspNode2, and divide portal 6 into portal 5 and portal 6.
Step 7
We find the second suitable triangle, and clip portal 6 into portal 6 and portal 7.
Step 8
We find the last suitable triangle in BspNode2, and clip portal 7 into portal 7 and portal 8.
Step 9
After deleting all the blue portals we get what we want, the yellow portal that connects BspNode1 and BspNode2.
Here is the detailed version:
void CBspTree::GeneratePortal(CBspTreeNode *pBspNode_, CSuperPlane *pSuperPlane_)
{
CPortal *pTemp1,*pTemp2;
int iCount;
if (pBspNode_->IsLeaf ())
{
if (!pSuperPlane_) return; //You should give us a bsp tree with more than 1 node!
for (each triangle T in pBspNode_)
{
iCount = pSuperPlane_->m_ListOfPortals.GetCount();
for (each portal P in pSuperPlane_->m_ListOfPortals)
{
iCount--;
if (iCount<0) break;
//please keep in mind,this process is
//to trace the validation of each portal
int *pInt;
if (P->m_iLeftNode == pBspNode->m_iTag)
pInt = &P->m_iLeftNode;
else if (P->m_iRightNode == pBspNode->m_iTag)
pInt = &P->m_iRightNode;
else continue; // P has no relationship with this pBspNode_,so just ignore P
if (TriangleIntersectPolygon(T,P->m_polygon))
{
pTemp1 = new CPortal;
pTemp2 = new CPortal;
pTemp1.m_bCulled = FALSE;
pTemp2.m_bCulled = TRUE;
ClipPortal(T->m_Plane, P,*pTemp1,*pTemp2);
if (!pTemp1->Reasonable()|| !pTemp2->Reasonable())
{
//Abort this operation
delete pTemp1;
delete pTemp2;
continue;
}
pSuperPlane_->m_ListOfPortals.Add(pTemp1);
pSuperPlane_->m_ListOfPortals.Add(pTemp2);
pSuperPlane_->m_ListOfPortals.Remove(P);
}
}
}
//OK,now we can delete those Culled portals in this leaf!
for (each portal P in pSuperPlane_->m_ListOfPortals)
{
if ((P->m_iLeftNode!=pBspNode_->m_iTag)&&
(P->m_iRightNode!=pBspNode_->m_iTag))
continue;
if (P->m_bCulled)
pSuperPlane_->Remove(P);
}
}
else
{
if (pSuperPlane)
{
iCount = pSuperPlane_->m_ListOfPortals.GetCount();
for (each portal P in pSuperPlane_->m_ListOfPortals)
{
iCount--;
if (iCount<0) break;
//please keep in mind,this process is
//to trace connection information of each portal
int *pInt;
if (P->m_iLeftNode == pBspNode->m_iTag)
pInt = &P->m_iLeftNode;
else if (P->m_iRightNode == pBspNode->m_iTag)
pInt = &P->m_iRightNode;
else continue;// P has no relationship with this pBspNode_,so just ignore P
switch (CalculateSide(pBspNode_->m_DividingPlane,&P->m_Polygon))
{
case Polygon is on positive side of the dividing plane:
*pInt = pBspNode_->m_pLeftNode->m_iTag;
break;
case Polygon is on negative side of the dividing plane:
*pInt = pBspNode_->m_pRightNode->m_iTag;
break;
case Polygon is spanning the dividing plane:
pTemp1 = new CPortal;
pTemp2 = new CPortal;
pTemp1->m_bCulled = P->m_bCulled;
pTemp2->m_bCulled = P->m_bCulled;
if (*pInt == pPortal->m_iLeftNode)
{
This means we only need to update the left connection information:
pTemp1->m_iLeftNode = pBspNode_->m_pLeftNode->m_iTag;
pTemp2->m_iLeftNode = pBspNode_->m_pRightNode->m_iTag;
pTemp1->m_iRightNode = pBspNode_->m_pRightNode->m_iTag;
pTemp2->m_iRightNode = pBspNode_->m_pRightNode->m_iTag;
}
else
{
This means we only need to update the right connection information:
pTemp1->m_iRightNode = pBspNode_->m_pLeftNode->m_iTag;
pTemp2->m_iRightNode = pBspNode_->m_pRightNode->m_iTag;
pTemp1->m_iLeftNode = pBspNode_->m_pLeftNode->m_iTag;
pTemp2->m_iLeftNode = pBspNode_->m_pLeftNode->m_iTag;
}
ClipPortal(pBspNode_->m_DividingPlane,P,*pTemp1,*pTemp2);
pSuperPlane_->m_ListOfPortals.Add(pTemp1);
pSuperPlane_->m_ListOfPortals.Add(pTemp2);
pSuperPlane_->m_ListOfPortals.Remove(P);
break;
case Polygon is coincide with the dividing plane:
This situation should not happen, but it could. If this happens, that
means your bsp tree is not organized well, for you have used a dividing
plane which almost coincide with another dividing plane on the parent
node. You should make sure your bsp tree is reasonable, or just do
nothing here.
break;
}
}
GeneratePortal(pBspNode_->m_pLeftNode,pSuperPlane_);
GeneratePortal(pBspNode_->m_pRightNode,pSuperPlane_);
}
if (!pBspNode_->m_bPushed) //we haven't generated a SuperPlane at pBspNode_
{
pBspNode_->m_bPushed = TRUE;
CPortal* pPortal = new CPortal;
CSuperPlane* pNewSuperPlane = new CSuperPlane;
m_ListOfSuperPlanes.Add(pNewSuperPlane);
On this superplane, generate a large enough polygon for the portal which exceeds the
boundary of the bounding box of the environment. In our method we use a rectangle,
but you can use other shapes as long as you meet the requirement. Then add those
points to pPortal->m_Polygon
In our assumption, the portals on the SuperPlane of pBspNode_ should only connect
the regions in the subtree of pBspNode_, so we should confine the polygon of portal
on the Superplane to the convex space of pBspNode_, this will optimize the
performance. We achieve this by cliping the polygon against all the planes that on
parent nodes of pBspNode_ as below:
CbspNode* pTempNode,pPrevNode
PPrevNode = pBspNode_;
for (pTempNode = pBspNode_->m_pParent;pTempNode!= NULL;
pTempNode = pTempNode->m_pParent)
{
if (pTempPortal is spanning the dividing plane of pTempNode)
{
ClipPortal(pTempNode->m_DividingPlane,pPortal,*pTemp1,*pTemp2);
if (pPrevNode == pTempNode->m_pLeftNode)
*pPortal = *pTemp1;
else
*pPortal = *pTemp2;
delete pTemp1;
delete pTemp2;
}
pPrevNode = pTempNode;
}
pNewSuperPlane->m_ListOfPortals.Add(pPortal);
Now get the connection information of the Portal we have just generated,
C3DPoint v1,v2,v3;
v1=pPortal->m_Polygon.m_pPoints[0]-pPortal->m_Polygon.m_pPoints[1];
v2=pPortal->m_Polygon.m_pPoints[2]-pPortal->m_Polygon.m_pPoints[1];
v1.Normalize();
v2.Normalize();
v3=CrossProduct(v2,v1);
if (DotProduct(v3, pBspNode->m_DividingPlane.Normal)>0)
{
The normal of the portal plane is the same as the normal of the dividing
plane of the pBspNode_
pPortal->m_iLeftNode = pBspNode_->m_pLeftNode->m_iTag;
pPortal->m_iRightNode = pBspNode_->m_pRightNode->m_iTag;
}
else
{
The normal of the portal plane is the opposite against the normal of the
dividing plane of the pBspNode_
pPortal->m_iLeftNode = pBspNode_->m_pRightNode->m_iTag;
pPortal->m_iRightNode = pBspNode_->m_pLeftNode->m_iTag;
}
Now the left thing is to push this superplane down to the subtree:
GeneratePortal(pBspNode_->m_pLeftNode,pNewSuperPlane);
GeneratePortal(pBspNode_->m_pRightNode,pNewSuperPlane);
}
}
}
Tolerance control
We will only discuss the primary situations here:
1.Function CalculateSide:
In this function, when we test point PT against plane PN, we use the following formula:
F= PT.x*PN.A+PT.y*PN.B+PT.z*PN.C+PN.D; //we use Ax+By+Cz+D=0 as the plane's equation
switch (F)
{
case > BSP_TOLERANCE:
return point is on positive side;
case < BSP_TOLERANCE
return point is on negative side;
default:
return point is on the plane;
}
After a great deal of experimentation we found that a BSP_TOLERANCE value of 1e-3 provides the best trade-off in our engine. (In our modelling, we treat 1 worldspace unit as 1 meter in the real world).
2. Function TriangleIntersectPolygon:
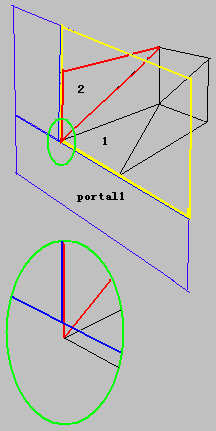You can never trust the result of your clip function!
See the image to the left. After triangle 1 clips the large portal, it seems correct to the casual observer, but if you zoom in the green circle you will find they don't match!
The image below illustrates what will happen if we don't use any tolerance control:
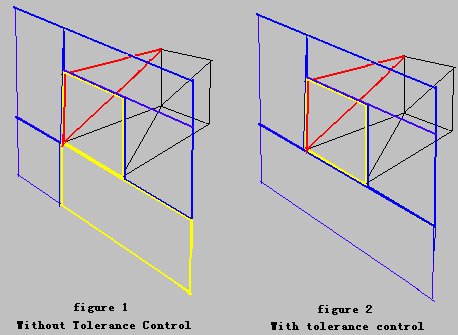
So, without tolerance control, the function will think triangle 2 intersects portal 1. Then when you use the plane of the triangle 2 to clip portal 1, you will make part of portal 1 valid as shown in figure 1, the yellow portal at the bottom.
In our algorithm, we regard the triangle and polygon as intersecting only when their intersection line segament exceeds a certain degree (i.e. BSP_TOLERANCE). You can use your own methods to do this test, and you may find other situations you need to handle, but it is not difficult once you know what you really want.
Last minute optimization
After generating portals, you may still get a few portals thant you don't want. The obvious ones are those portals on the walls. During the automatic generation process we don't handle this problem, since it seems better to handle it at a later stage. You also need to add some other rules to automatically eliminate obvious redundant portals generated by various errors. In our implementation we use an elimination process following the genneration process to check those portals against all the rules we have defined.
Another optimization we could add is to optimize the shape of the portal polygon. We should at least merge adjacent portals which have the same connection attribute and can form a single convex polygon. If the portal polygon has too many edges, you might prefer to use a simple shape such as a quadrangle to approximate the portal shape. This will increase the efficiency of rendering process.
Conclusion
To generate perfect portals in any environment is a very difficult problem (and is often impossible). However our goal was to make this process acceptable and save our artists' time as much as possible, which is a more reasonable goal.
The quality of the models comprising the scene and the quality of the BSP tree will heavily affect the quality of the portals generated by this method. 3dsmax is not high precision software - we will always find some trivial triangles the artists' work (i.e. those triangles not worth rendering). BSP generation can also create this kind of triangle if you don't handle it carefully. So further improvements can be made in these areas; you can add a preprocessing step to optimize these triangles - elimiating them or merging them with other triangles before starting the portal generation process.
Appendix
Here are some screenshots from our map editor. All models were made by 3dsmax.
 |
 |
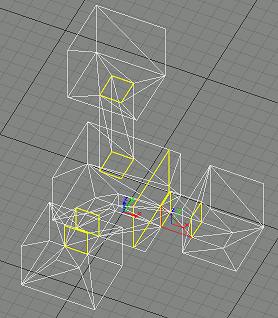If you have any questions or you have got some nice ideas to improve this algorithm, feel free to contact us.
Discuss this article in the forums
Date this article was posted to GameDev.net: 3/18/2003
(Note that this date does not necessarily correspond to the date the article was written)
See Also:
Algorithms and Data Structures
Featured Articles
© 1999-2011 Gamedev.net. All rights reserved. Terms of Use Privacy Policy
Comments? Questions? Feedback? Click here!