Procedural Planets Part 1 - Structure
by Andrew True

This article covers a triangle tessellation/data structure for procedural meshes that is different from the usual RTIN roams and significantly different from Diamond LoDs. These meshes can dynamically increase and decrease their level of detail dependant on the observers viewpoint, not drawing unnecessary detail if the observer cant see it, the essence of a procedural universe. This structure is something I've worked on for Entropy and is a non-RTIN equilateral spiral wound view dependant mesh. It's perfectly happy with open and closed structures. Incidently I am 99% certain (without access to source) that it is exactly how Frontier: First Encounters tessellates its planets.

I haven't written an article like this before, so I'm not entirely sure how to pitch it, how technical to get, how simple to keep it etc. I think familiarity with other LoD structures would probably be helpful, and rudimentary knowledge of vector math for some of the code. Tesselation wise though, you should be able to follow it without any real knowledge of 3d math. I've avoided dealing with texturing, and the procedural fractal/noise algorithms driving data for a planet, as that's the subject for another article. Here we'll concentrate on a sphere, because even without driving data the radial displacement makes for t-junctions, the avoidence of which is part of this article.

Finally there are some obvious and not so obvious optimizations which I only briefly touch upon, which I utilize in Entropy. The result of these make a fast tessellation extremely fast. This method also very quickly tessellates out new lod data with fewer operations than rtin-roam, and can be slightly tweaked to provide triangle strip/fan output without having to 'worm' the LoD to find them. In addition to indexing, very quick indeed.

Data Structure

Our data structure starts with a basic triangle. This structure uses Equilateral triangles. Although during the course of tessellation they will twist slightly through their plane due to the mid-point displacement, they retain equilateralism as viewed towards the center of the sphere along a normalized triangle centric point. The distortion is self correcting and works itself out, so theres no need to worry about it here. The only consequence is you can not just take the length of an edge and assume it still holds true for the other two edges, which would be important if your determination to split triangles was based upon your distance to them and the length of an edge. Rather handily, by choosing to base the decision off lower or higher edges (in terms of radial height), you can decide how tessellated vertical triangles such as cliffs will/wont become to some degree. Anyhow, thats something for part 2 where we deal with LoD driving.

These triangles can undergo two different types of LoD operation. They may be Split (into 4 child triangles) or Combined(into their parent if they have one). So each triangle contains four Child pointers, and one Parent pointer.

Because were dealing with the tessellation of a surface, and because there can be various sizes of triangle adjacent to one another, we need to keep track of these adjacencies. So each triangle has three Edge pointers, which point to neighboring triangles. Of these pointer types, children, parent and edges, only children are ever constructed into new triangles. And only children ever have delete called upon them. Its vital that whenever children are deleted their pointers are set to NULL. The structure is so interdependent that forgetting a simple thing like this can cause catastrophic recursion and/or crashes. This is because our Splitting function will recurse about these edges sometimes (though with less recursion that ROAM typically).

Lastly, our triangles should be nodes in a doubly linked-list. I wont go into the code for those here, I guess you could also use STL but I typically find a fairly straight forward implementation to be faster than the STL templates.

class cLoDTri;
{
  dVector p[3]; //points
  cLoDTri* e[3]; //edges
  cLoDTri* pParent; //parent
  cLoDTri* child[4]; //children
}

For our tessellation structure we have a few very strict rules.

A triangle must be neighbored by a triangle no bigger than our parent.
If we don't have a neighbour (parents neighbour is bigger or has grandchildren), we point to NULL;

A Math-Magic Relationship

In our triangle data structure we have an array of points (p[3]), children (child[4]) and edges (e[3]). Because the triangles are equilateral, there's no guarantee of the orientation of a neighbour relative to t. Rather than trying to track the orientations of all the triangles as down, up-left, up-right etc, and derive specific cases for the interactions between them based on that (which you need to do if you had ordered the points,children, and edges left to right), our counter-clock spiral ordering gives us a unique and simple relationship, though its not immediatly obvious.

int j=i+1; if(j>2) j=0;

This relationship, with a point, edge, or child index into the appropriate array plugged into i, and the result j, gives us some noteworthy results.

If i is an edge, i and j are the appropriate points making that edge.
If i is a edge, i and j are the appropriate children along that edge, and i is the edge each child shares with its parent.
If i is a point, j is the counter clock-wise point.

Splitting Triangles

void cLoDManager::Split( cLoDTri* t );

Firstly, Split() being a recursive function, we need to return without action if t is null. It's faster than checking in the calling function the state of t. Then we go through the edge pointers of t. Any edges that are set to NULL indicate a triangle off that edge that is larger than us. Think about this for a moment, if there is a triangle next to us with children, our edge pointer will point to their parent. If it is the same as us, we will also be pointing to a neighboring tri. The only case where no neighbour exists is if we are higher detail than it. Seen as we have a rule, the same rule that ensures this relationship, we Split t->e[n] before we can split ourselves, ensuring that triangles remain within one order of detail of their neighbors.

That done, we create three new points, each along the midpoint of our edges.

dVector n[3];
n[0] = t->p[0].vMidpoint(t->p[1]);
n[1] = t->p[1].vMidpoint(t->p[2]);
n[2] = t->p[0].vMidpoint(t->p[2]);

These midpoints are what we will use to make our 4 child triangles. These midpoints are the sum of the two points / 2. Note this means even with our four children the mesh of four triangles is flat. We need to normalize each midpoint and multiply it by the radius of the sphere. This provides the spherical displacement. But we can't do that yet. If we do we get the following nasty result.

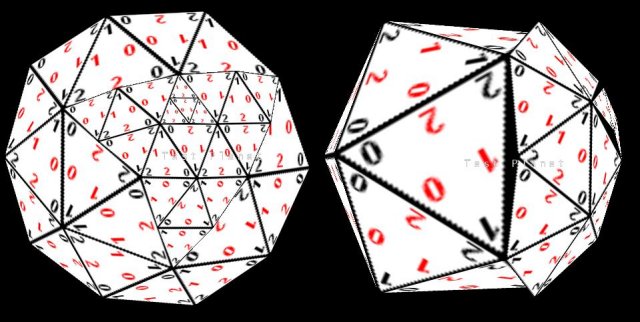
There are a few ways to close these gaps. Most of them are very inefficient. The methods I've seen used, eg in Diamond Roam, are to bridge our now larger neighbors points with our displaced midpoint in as few a tessellations as possible. There are 3*2 permutations of this bridging, and it requires excessive management to cope with. Somewhere to keep the hybrid split tris and/or more heinously, determining them during the rendering cycle. It's this that puts people off equ-lods :p Although this method is achievable a little easier with the Magic-Relationship as (ok, really it's with the counter-clock spiral ordering) we remove triangle orientation complications (only 2 permutations of the bridging remain), there's a much simpler and faster solution.

Don't fill gaps, don't have gaps!

We only perform the displacement if our neighbour has children. Additionally, we tell the neighboring children that share this point, they can now be displaced, as it's guaranteed they haven't been if we're not split yet. Worth noting is the above code becomes one very simple line once you index your mesh, as you don't need to use the magic-relationship to seek out the point on each triangle, you just need to find it for one.

for(int i=0; i<3; i++)
{
  //here, even if were not raising the point to the radius+detail,
  //prepare the texturing, colouring etc as if we were
  //...
  if(t->e[i]->bHasChildren())
  {
    n[i].vNormalize(); n[i] *= radius;
    //and tell neighboring children sharing point they can raise from midpoint
    int it0=t->e[i]->iSharesEdge(t);
    int it1=it0+1; if(it1>2)it1=0;
    int it3=it1+1; if(it3>2)it3=0;
    t->e[i]->child[it0]->p[it1]=n[i];
    t->e[i]->child[it1]->p[it0]=n[i];
    t->e[i]->child[3]->p[it3]=n[i];
  }
}

Now we can construct our children and set up our child, parent pointers.

t->child[0] = new cLoDTri(t->p[0],n[0],n[2]);
t->child[1] = new cLoDTri(n[0],t->p[1],n[1]);
t->child[2] = new cLoDTri(n[2],n[1],t->p[2]);
t->child[3] = new cLoDTri(n[1],n[2],n[0]);

for(int i=0;i<4;i++)
  t->child[i]->pParent=t;

t->child[0]->e[1]=t->child[3];
t->child[1]->e[2]=t->child[3];
t->child[2]->e[0]=t->child[3];

"Neighbour's... Everybody needs good..."

We can also set up child[3]'s edge pointers as it simply points to the other children.

t->child[3]->SetEdgePointers(t->child[2],t->child[0],t->child[1]);

Setting up the other children's edge pointers is slightly less trivial because of the variable orientations of neighboring tris. Rather than use a big switch() setup dealing with the neighbor orientations on a case by case business though, the math-magical relationship saves us again and makes it trivial (and plenty fast enough for a split operation).

for(int i=0; i<3; i++)
{
  if(t->e[i]) //non-closed surface trap
  if(t->e[i]->bHasChildren())
  {
    //triangle has children we can point our children too.
    int j=i+1; if(j>2) j=0;
    int sharedEdge=t->e[i]->iSharesEdge(t);
    if(sharedEdge!=-1)
    {
      int k=sharedEdge+1; if(k>2)k=0;
      t->child[i]->e[i]=t->e[i]->child[k];
      t->child[j]->e[i]=t->e[i]->child[sharedEdge];
      t->e[i]->child[sharedEdge]->e[sharedEdge]=t->child[j];
      t->e[i]->child[k]->e[sharedEdge]=t->child[i];
    }
  }
}

the function iSharesEdge is simply defined as:

int cLoDTri::iSharesEdge(cLoDTri* t)
{
  for(int i=0;i<3;i++)
    if(e[i]==t) return i;
  return -1;
}

This is fairly intuitive if you stare at the diagram for a little while. All thats left is to put the children into the mesh, and take the parent out.

m_llMesh.AddHead(t->child[0]);
m_llMesh.AddHead(t->child[1]);
m_llMesh.AddHead(t->child[2]);
m_llMesh.AddHead(t->child[3]);

t->Remove();
m_llParents.AddHead(t);

"From up here, I can see the big picture"

Combining triangles is the opposite of splitting them. Our mesh simplifies back, though in the case of a planet you probably don't want it to simplify back to the original polytope. Thats a discussion for the next article though. Combining is fortunately, very straight-forward (if you got this far).

Fundamentally you just delete the children, and remove the parent from the parent list and put it back in the mesh. Like splitting a triangle, theres some bookkeeping to do with the edges and displacements again, but its much more trivial. Also, Combines are not iterative like Splits. Only the triangle we're looking at is operated upon. They must also be parents or there's nothing to combine.

We can only combine a triangle if it has children, but no grandkids. You'd think looking at a diagram that there was more involved, like neighbors with grandchildren, but you'll easily note that a neighbour with grandchildren adjacent to any of our edges means we must also be at that level of detail, ie. We wouldn't be here trying to combine this triangle, we'd be further down the sibling list trying to combine one. Trust me, it works.

//if t has no children return immediately, no merge
if(!t->bHasChildren()) return;

//if t has grandchildren, return, cant merge
for(int i=0; i<4; i++)
  if(t->child[i]->bHasChildren()) return;

The rest is nothing you haven't seen yet but in reverse. The only noteworthy point here you might forget is that you have to tell neighboring displacements that they must be flat again, or you'll see a gap. Again the spiral counter-clock winding saves us massive switch() case by case algorithmic orientation checks.

//we got this far we can do the combine
for(int i=0; i<3; i++)
{
  //any neighbors with children, inform them our children
  //are gone (point them to null)
  if(t->e[i]->bHasChildren())
  {
    int iEdge=t->e[i]->iSharesEdge(t);
    if(iEdge!=-1)
    {
      int j=iEdge+1; if(j>2)j=0;
      t->e[i]->child[iEdge]->e[iEdge]=NULL;
      t->e[i]->child[j]->e[iEdge]=NULL;

      //correct neighbour child's points
      dVector n = 
        t->e[i]->child[iEdge]->p[iEdge].vMidpoint(t->e[i]->child[j]->p[j]);
      int l=j+1; if(l>2)l=0;
      t->e[i]->child[iEdge]->p[j] = n;
      t->e[i]->child[j]->p[iEdge] = n;
      t->e[i]->child[3]->p[l] = n;
    }
  }
}

//delete our children
for(int i=0; i<4; i++) 
{
  delete t->child[i];
  t->child[i]=NULL;
}

//put triangle back into the mesh
t->Remove();
m_llMesh.AddHead(t);

Needing something to tessellate?

We need a surface to tessellate, a starting structure of equilateral triangles (it works without equilateral triangles but the distortion isn't pretty). In this case, Planets, we will start with an Icosahedron. There is a lower order polytope that would do, the ecohedron, but if you think about an ecohedron for a moment (two pyramids glued together), they have no equator, only poles. The triangles about the poles are manifold, in that the four triangles that make up each 'hemisphere' are initially anchored together at a shared polar point. This creates an unwelcome distortion in the tessellated mesh.

As an aside for a moment, as you will see the mesh deals automagically with NULL edge pointers, so this will happily tessellate any open or closed mesh. Its very handy in that respect for planetary ring systems, sheet nebulae etc.

I hard code this initial shape into the cLoDManager class. Its fairly straight forward so I'll just reproduce it here without much further explanation. The only change to this is if you were to index this mesh. I haven't done for clarity, though in my own implementations for Entropy I do it for the rendering performance. It also mildly optimizes the Split function.

void cLoDManager::BuildPlatonicPolytope()
{
  /* 20 equilaterals (icosahedron)
  http://astronomy.swin.edu.au/~pbourke/polyhedra/platonic/index.html
  */

  helper_tex.LoadUTGA("textures/orient.tga",false);

  radius=10;
  double a,b,phi;
  phi=(1+sqrtf(5))/2;
  a = 0.5; b = 1 / (2 * phi);
  dVector p[60];
  p[0]=dVector(0, b, -a);  p[1]=dVector(b, a, 0);   p[2]=dVector(-b, a, 0);
  p[3]=dVector(0, b, a);   p[4]=dVector(-b, a, 0);  p[5]=dVector(b, a, 0);
  p[6]=dVector(0, b, a);   p[7]=dVector(0, -b, a);  p[8]=dVector(-a, 0, b);
  p[9]=dVector(0, b, a);   p[10]=dVector(a, 0, b);  p[11]=dVector(0, -b, a);
  p[12]=dVector(0, b, -a); p[13]=dVector(0,-b, -a); p[14]=dVector(a, 0, -b);
  p[15]=dVector(0, b, -a); p[16]=dVector(-a, 0,-b); p[17]=dVector(0, -b,-a);
  p[18]=dVector(0, -b, a); p[19]=dVector(b,-a, 0);  p[20]=dVector(-b,-a, 0);
  p[21]=dVector(0, -b,-a); p[22]=dVector(-b,-a, 0); p[23]=dVector(b,-a, 0);
  p[24]=dVector(-b, a, 0); p[25]=dVector(-a, 0, b); p[26]=dVector(-a, 0, -b);
  p[27]=dVector(-b,-a, 0); p[28]=dVector(-a, 0,-b); p[29]=dVector(-a, 0, b);
  p[30]=dVector(b, a, 0);  p[31]=dVector(a, 0,-b);  p[32]=dVector(a, 0, b);
  p[33]=dVector(b, -a,0);  p[34]=dVector(a, 0, b);  p[35]=dVector(a, 0,-b);
  p[36]=dVector(0, b, a);  p[37]=dVector(-a, 0, b); p[38]=dVector(-b, a, 0);
  p[39]=dVector(0, b, a);  p[40]=dVector(b, a, 0);  p[41]=dVector(a, 0, b);
  p[42]=dVector(0, b,-a);  p[43]=dVector(-b, a, 0); p[44]=dVector(-a, 0,-b);
  p[45]=dVector(0, b,-a);  p[46]=dVector(a, 0,-b);  p[47]=dVector(b, a, 0);
  p[48]=dVector(0, -b,-a); p[49]=dVector(-a, 0,-b); p[50]=dVector(-b,-a, 0);
  p[51]=dVector(0, -b,-a); p[52]=dVector(b,-a, 0);  p[53]=dVector(a, 0,-b);
  p[54]=dVector(0, -b, a); p[55]=dVector(-b,-a, 0); p[56]=dVector(-a, 0, b);
  p[57]=dVector(0, -b, a); p[58]=dVector(a, 0, b);  p[59]=dVector(b,-a, 0);

  for(int k=0; k<60; k++) {
    p[k].vNormalize();
    p[k]*=radius;
  }

  cLoDTri* t[20];

  int j=0;
  for(int k=0; k<20; k++)
  {
    t[k] = new cLoDTri(p[j],p[j+2],p[j+1]);
    j+=3;
    m_llMesh.AddHead(t[k]);
  }

  /*build initial neighbour pointers iteratively. Only needs
    done at lowest lod, subsequently split~combine algorithm does it
    automatically and quickly (this is slow for higher lod, but fast
    enough for this primitive)*/
  for(cLoDTri* tl = m_llMesh.GetHead(); tl->InList(); tl = tl->GetNext())
  for(cLoDTri* tn = m_llMesh.GetHead(); tn->InList(); tn = tn->GetNext())
    if(tl!=tn)
    {
      for(int i=0; i<3; i++)
      {
        int j=((i+1)>2)?0:(i+1);
        if(tn->SharesPoint(tl->p[i]) && tn->SharesPoint(tl->p[j]))
        {
          tl->e[i]=tn;
        }
    }
  }
}

Conclusion

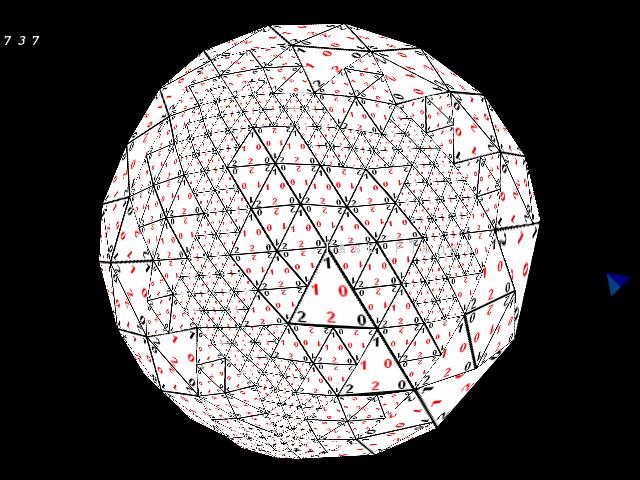
Below is an executable that you can play around with to see the mesh in action. It's not a fully scaled planet, more like an interactive diagram. It makes the structure and tessellation method very plain to see.

Requires OpenGL, Win32.

Right mouse button rotates you around the lod, mousewheel zooms you in and out.

Download(139kb)

My Homepage

Discuss this article in the forums

Date this article was posted to GameDev.net: 3/21/2004
(Note that this date does not necessarily correspond to the date the article was written)