Introduction

I'm often asked about collision detection for games, where a player can collide with a static environment. I figured it was time to write a document, so I present you with this, very informal and in my own words.

This document will describe a collision technique that allows you to move an ellipsoid (a sphere with three different radii, one for each axis) through a world that not only properly detects collisions, but also reacts in a way that gamers would expect from the common first person shooter.

This technique also allows for sliding along surfaces as well as easy implementation of gravity, which includes sliding downhill when standing stationary. This technique also allows automatic climbing of stairs and sliding over bumps in walls (like door frames) and any other randomly oriented "stair-like topography".

Defining Some Terms

Just so we’re all on the same starting page, I’ll define three basic terms:

Source - The source point where a colliding object starts. Every colliding object travels from the source to a collision on its way to the destination.

Destination - This is where the colliding object wants to go to, but can’t get there, because it’s too busy bumping into stuff.

Velocity vector - This is the vector that defines the direction and speed that the colliding object is traveling. If a colliding object is traveling two feet forward, then the direction of this vector is forward, and the length of this vector is two feet.

Starting Simple: Spheres And Planes Only

I’m going to start simple by dealing with spheres and planes only. We’ll get to ellipsoids and polygons soon enough.

Before we can really dig in, we’ll need to determine the intersection of a ray with a plane. Here’s some pseudo code:

// Inputs: plane origin, plane normal, ray origin ray vector.
// NOTE: both vectors are assumed to be normalized

double intersect(Point pOrigin, Vector pNormal, Point rOrigin, Vector rVector)
{
   double d = -(planeNormal * planeOrigin);
   double numer = planeNormal * rayOrigin + d;
   double denom = planeNormal * rayVector;
   return -(numer / denom);
}

Colliding A Sphere With A Plane

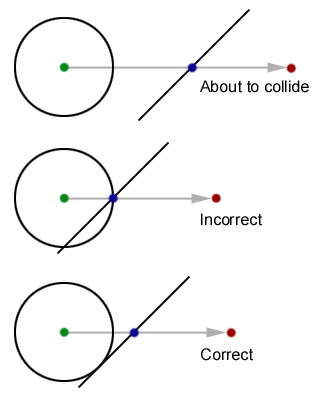
Figure 1 shows that our task isn’t as simple as determining where the velocity vector intersects the plane. As you can see, this causes an incorrect collision because the sphere passes through the plane at a point other than the ray/plane collision point. Let’s take a closer look at the correct collision:

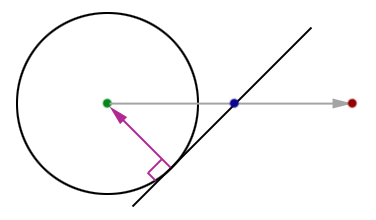
In figure 2, you can clearly see that the vector formed by the point of intersection and the center of the sphere, is coincident with the plane’s normal. We can reverse this process to determine the point on the surface of the sphere that will intersect with the plane before we even do the collisions. That’s a bit confusing, so here’s a helping of visual aid:

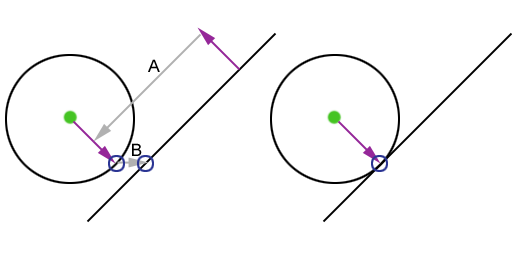
Figure 3 shows that the plane’s normal can be used to determine the point on the surface of the sphere that will eventually intersect the plane. We’ll call this point the sphere intersection point.

We do this by first setting the length of the plane’s normal to the radius of the sphere, and then we invert it. Following the gray line (labeled ‘A’) you can clearly see that the result is a vector that (when added to the center point of the sphere) results in the sphere intersection point.

From this point, we move along our velocity vector (the gray line labeled ‘B’), until we intersect the plane. The latter half of the example shows the final result – our sphere sits nicely on the plane.

If the plane bisects the sphere, we’ll end up with a sphere intersection point that is on the backside of the plane.

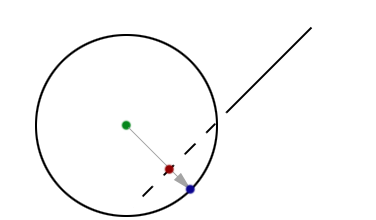
Figure 3a shows an embedded plane. Because of this, our sphere intersection point is beyond the plane, causing our collisions to fail.

To solve this problem, we first need to detect this case. We do so by determining the distance from the origin of the sphere to the plane. We trace a ray from the origin of the sphere toward the plane, along the plane’s inverted normal (the gray vector shown in Figure 3a.) This results in the plane intersection point (the red point in Figure 3a.) If the distance from this point to the origin of the sphere is less than the radius of the sphere, we have an embedded sphere, and this becomes our plane intersection point. We then continue as normal and determine the polygon intersection point.

Colliding With Multiple Planes

At this point in time (it’s a point as good as any :), I should mention that if you are colliding with a plane, and that plane’s normal faces away from the sphere (i.e. the dot product between the velocity vector and the plane’s normal is > 0) you will want to ignore that plane.

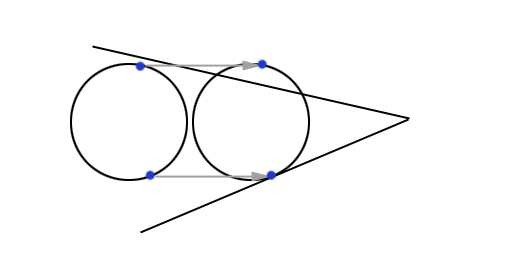
Figure 4, aside from being an optical illusion (both circles really are the same size), shows us that we need to be careful when there is more than one potentially colliding plane in our path.

The solution to this is simple… we merely need to consider all potential colliders and determine which one collides first…

Determining Potential Colliders

The method by which you chose to do this depends on your dataset, how it’s organized, how you deal with collisions, and a whole lot more. But here’s a simple solution that covers most cases:

1. Find the bounding box of your sphere, centered on the source position
2. Find the bounding box of your sphere, centered on the destination position
3. Find the bounding box of those two bounding boxes
4. Find all polygons that intersect that final bounding box

Be careful on #4! Finding a polygon that intersects the bounding box is not as simple as it seems… you can’t just look for vertices in the box, since there will often be times when a polygon’s vertices are all outside of a box, yet the polygon still intersects the box (consider a huge polygon with a tiny box that intersects the polygon near its center.) Properly doing this requires clipping the polygon to the box.

Getting Ready to Collide With Polygons

Until now, I’ve tried to stick to dealing only with collisions with planes. If our scene was as simple as a single convex space we could stop here, but few scenes are. Here’s an example of what you might run into if you only try to collide with planes rather than polygons, in a non-convex space:

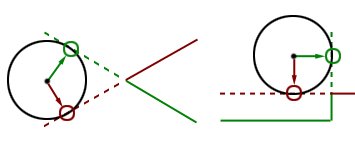
Figure 5 is a clear example of two cases that show the difference between polygon and plane collisions.

At some point, we’ll need to know which point inside the polygon is closest to our intersection point on the plane. Since the polygon and the intersection point both lie on the plane, this problem may be as simple as determining if our intersection point is within the polygon. If so, then our intersection point is the closest point in the polygon. However, often times, our intersection point will lie beyond the extents of the polygon (as shown in both cases of figure 5). In this case, the closest point in the polygon will lie on its perimeter.

So, it’s time to find the closest point on a polygon’s perimeter to a point.

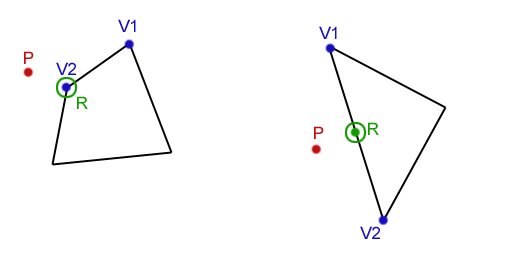
In the above example we show the closest point (R) to P. R is always on the perimeter of the polygon. The first step in solving this problem is to determine the closest point on a line to P. This is performed for each edge of the polygon and the closest resulting point from each edge is the winner. We call this resulting point ‘R’. Here’s an example that shows how to determine the closest point on a triangle’s perimeter to a point on its plane:

Point  closestPointOnTriangle(Point a, Point b, Point c, Point p)
{
   Point  Rab = closestPointOnLine(a, b, p);
   Point  Rbc = closestPointOnLine(b, c, p);
   Point  Rca = closestPointOnLine(c, a, p);
   return closest [Rab, Rbc, Rca] to p;
}

 

Point  closestPointOnLine(Point a, Point b, Point p)
{
   // Determine t (the length of the vector from ‘a’ to ‘p’)

   Vector c = p - a;
   Vector V = Normalized vector [b – a];
   double d = distance from a to b;
   double t = V * c;

   // Check to see if ‘t’ is beyond the extents of the line segment

   if (t < 0) return a;
   if (t > d) return b;
 
   // Return the point between ‘a’ and ‘b’

   set length of V to t;
   return a + V;
}

Our Goal

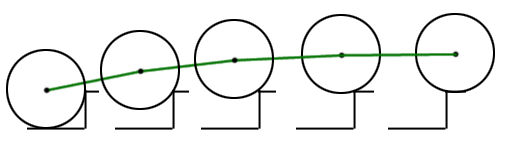
Figure 7 shows five consecutive samples of a sphere climbing stairs. Note the green curve showing the path of the sphere. This curve allows our sphere to move about the environment in a smooth way, not jumping up stairs but rather rolling up them, in a way that a ball naturally would. Consider the following example:

If you were to place a beach ball in front of a wall that was taller than the ball, you would not be able to push the ball forward (the wall’s height is taller than half the ball’s height.) However, if you were to place the ball in front of a stair that was slightly less than half the ball’s height and push the ball directly at the stairs (horizontally) you would notice that as you pushed the ball, it would begin to slowly move forward, climbing the stair as it did. Yet as the ball started to crest the top of the stair, you wouldn’t have to push quite as hard to keep the ball moving. By the time the ball reaches the top of the stair, it will roll freely.

The movement doesn’t only follow a curve, but so does the amount of force required to push the ball up the stair.

Let’s now extend this to a common game environment scenario, with a 6-foot ball, and a 1-foot stair. Referring to our real-world example, the ball would roll up the stairs with a nice smooth motion as it crested each stair, because the ball is so much taller than the stair. This is the effect we plan to achieve.

Colliding With Polygons

Finding the intersection of the ray/plane doesn’t give us enough information, since (as shown in figure 5) that point may not lie within the polygon (thus, it is termed the Plane Intersection Point). We’ll need to determine if this collision point is within the polygon and if not, determine the nearest point on the polygon’s perimeter to this point. This will become our Polygon Intersection Point.

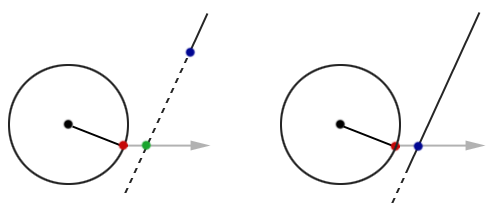
Figure 8 (left) shows us that if we use the sphere intersection point to determine the intersection with the plane (along the direction of the velocity vector) we get a point, which lies on the polygon’s plane yet lie outside the polygon (the plane intersection point). What we really want is the polygon intersection point. To find this, we must determine the point on the polygon’s perimeter that is nearest to the plane intersection point.

Figure 8 (right) shows us that the intersection with the polygon’s plane results in a point within the polygon, so there is no need to determine the nearest point on the polygon’s perimeter. In this case, the plane intersection point and the polygon intersection point are one in the same.

Also note that the polygon intersection point in figure 8 (left) will never intersect our sphere. So our next step is to determine where the sphere will intersect our polygon intersection point (if at all).

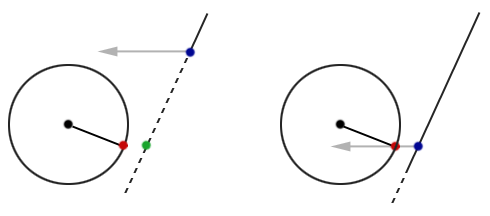
Figure 9 shows us that if we reverse the direction of the velocity vector, we can detect the point of collision with the sphere – we’ll call this reverse intersection. To do this, we will need a ray/sphere intersection routine. In each case, our ray will originate from the polygon intersection point. Also note that in figure 9 (left) it has become clear that our sphere will never intersect the polygon.

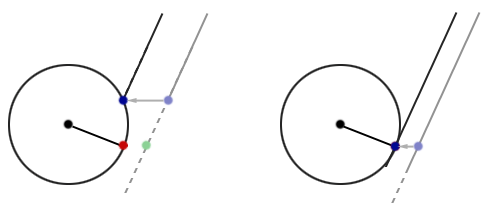
Figure 10 shows two cases in which the polygon intersection point is used for reverse intersection to locate the point at which a collision with the sphere occurs. Note that in figure 10 (right) this point is the same point as the sphere intersection point; yet figure 10 (left) it is not.

Here’s an example of the ray/sphere intersection (the inputs are the ray’s origin and normalized direction vector, as well as the sphere’s origin and radius):

double intersectSphere(Point rO, Vector rV, Point sO, double sR)
{
   Vector Q = sO - rO;
   double c = length of Q;
   double v = Q * rV;
   double d = sR*sR - (c*c – v*v);

   // If there was no intersection, return -1

   if (d < 0.0) return -1.0;

   // Return the distance to the [first] intersecting point

   return v - sqrt(d);
} 

Sliding

Until now, we’ve only talked about how to deal with collisions. Any physics expert will tell you that the velocity vector represents energy in the form of momentum. Once a collision happens, there is leftover energy (the remaining distance to the destination.) Some of that energy is absorbed in the collision (this varies with the angle of incidence of the collision.) You can do whatever you want with this leftover energy, like bouncing and sliding. I’ll cover sliding since it’s the most popular.

Sliding, at its simplest form is done along a sliding plane.

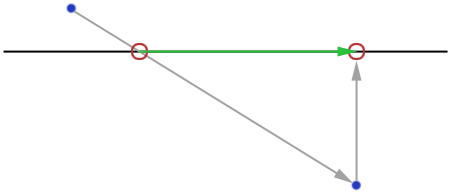
Figure 11 illustrates the process of sliding. First, a collision is detected, and the velocity vector (the long diagonal gray line) is cut short at the point where it collides with the plane. The remainder (the leftover energy – everything behind the plane) is not thrown away. Rather, the destination point is projected onto the plane along the plane’s normal. This new point, subtracted from our collision point results in a new velocity vector that can be used for sliding.

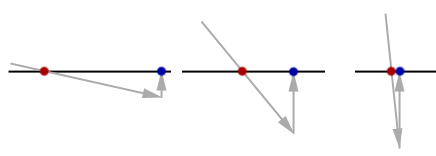
Figure 12 shows us that, as stated earlier, the distance to slide will vary with the angle of incidence, even thought the initial velocity vectors are very similar in length.

We can’t merely slide right along, oblivious to the rest of the world. If our velocity vector is long enough, we may slide for quite a distance, in which case we may collide with more geometry. So rather than sliding right along, we’ll simply pass this new vector (the slide vector) through our entire collision routine.

Before we can determine the sliding vector, we need to calculate our sliding plane.

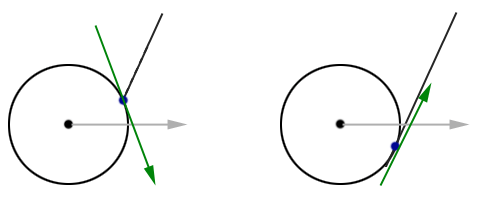
The sliding plane, like any plane, is defined by an origin (a point) and a normal. The origin to the sliding plane is the point of intersection with the sphere. The normal of this plane is the vector from the intersection point to the center of the sphere.

As stated earlier, we will need to project our destination point onto the sliding plane. This can be done with a simple ray/plane intersection, where the ray’s origin is the destination point, and the ray’s normal is the normal of the sliding plane.

There is a pretty cool effect that we can achieve by doing this. If our velocity vector is long enough, we can slide along multiple surfaces. This is possible if our sliding vector so long, that it causes a collision with another angular surface, which in turn, causes us to slide along it. If the initial velocity vector was long enough, we could end up sliding right around the inside of a rounded corner. This is similar to a hockey puck traveling at a high velocity, sliding around the back corner in a hockey rink.

You can take friction into account by simply shortening the slide vector to some degree. One way to do this is to associate a friction with each surface in the scene. When you collide with a surface, keep track of its friction. Before you slide, apply that friction to the sliding vector.

Gravity

Adding gravity is a no-brainer. Start by determining your gravity vector. In the case of a standard world, your gravity vector might be [0, -1, 0] (straight down). You can increase or decrease your gravity by lengthening or shortening the gravity vector. In this case, [0, -1000, 0] would be quite a lot of gravity, and [0, -0.00001, 0] would be very little gravity. Of course, the amount of gravity you apply needs to be directly proportional to your unit system.

To apply gravity, simply add it to the initial velocity vector that gets passed into your collision routines. Be careful not to add it to the sliding vectors, or you’ll get perpetual motion, because you’ll always have “leftover energy” and will end up perpetually sliding.

Gravity vectors don’t need to point straight down. If you’re an Escher fan, you might consider pointing them up, or at some other angle. :)

Sliding Downhill Is Automatic

The gravity vector, just like real gravity, is constant. It’s always present, even when the colliding object is standing still.

Because of this, if the colliding object is on a slanted ground, there is still a force of gravity being applied. This, combined with proper sliding will cause the player to slide down slopes automatically.

If you don’t like this, you can prevent it with the use of friction (as mentioned earlier) or by not applying gravity when the colliding sphere is stationary.

Making It Ellipsoidal

The radius for an ellipsoid cannot be defined by a single value. Rather, it is defined by something called the radius vector. For an ellipse (the 2D version of an ellipsoid), the radius vector might look something like this:

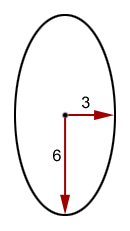
Figure 14 shows an ellipse with a radius vector of [3,6]. This results in an ellipse that is 6 units wide and 12 units tall.

If you were to add any unit vector to a point, you would end up with a point on the surface of a unit sphere, centered on that point. If you were to scale that unit vector by the radius vector of an ellipsoid, you would end up with a point on the surface of that ellipsoid.

Here’s an example in two dimensions:

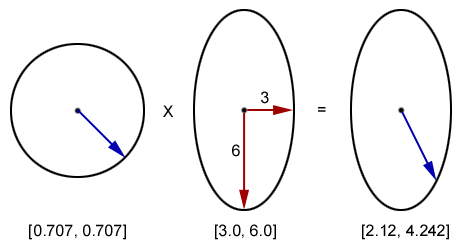
Figure 15 shows a unit circle with the vector [0.707, 0.707] – a 2-dimensional unit vector. When multiplied (component wise) by our radius vector [3, 6] we end up with a new vector [2.12, 4.242], which is then used to scale the circle to an ellipse. This, of course, extends perfectly into three dimensions.

In an earlier section, we discussed how to calculate the sphere intersection point by inverting the plane’s normal, setting its length to the radius of the sphere and adding this to the center point of the sphere. We’re going to change this just a little. For ellipsoids, we’ll use the plane’s normal (a unit vector) invert it, scale it by the radius vector and finally add it to the source point. This results in our ellipsoid intersection point. This is a rather small change, which allows us to use ellipsoids rather than spheres for our calculations.

Before we can consider our collisions with ellipsoids complete, we must also remember that our ray/sphere intersection must really be a ray/ellipsoid intersection.

Thus, we are now able to collide with ellipsoids, rather than simple spheres. Sliding, gravity, everything else continues to work the same.

Summary: Tying It All Together

At this point, we’ve discussed all the tools needed for collision detection. Now we’re going to pull all these pieces together to make one coherent concept, which accomplishes our goal. I’ve chosen pseudo code for the task.

There’s one note about the following code: the intersect() routine assumes that the input direction vector for the ray is not normalized (thus, it does the normalization with itself.)

// The collision detection entry point

collisionDetection(Point sourcePoint, Vector velocityVector, Vector gravityVector)
{

   // We need to do any pre-collision detection work here. Such as adding
   // gravity to our veoclity vector. We want to do it in this
   // separate routine because the following routine is recursive, and we
   // don't want to recursively add gravity.

   velocityVector += gravityVector;
   call collideWithWorld(sourcePoint, velocityVector);
}


// The collision detection recursive routine

collideWithWorld(Point sourcePoint, Vector velocityVector)
{
   // How far do we need to go?

   Double distanceToTravel = length of velocityVector;

   // Do we need to bother?

   if (distanceToTravel < EPSILON) return;

   // What's our destination?

   Point  destinationPoint = sourcePoint + velocityVector;

   // Whom might we collide with?

   List   potentialColliders = determine list of potential colliders;

   // If there are none, we can safely move to the destination and bail

   if (potentialColliders is empty)
   {
      sourcePoint += velocityVector;
      return;
   }

   // Determine the nearest collider from the list potentialColliders

   bool   firstTimeThrough = true;
   Double nearestDistance = -1.0;
   Poly   nearestCollider = NULL;
   Point  nearestIntersectionPoint = NULL;
   Point  nearestPolygonIntersectionPoint = NULL;

   for (each polygon in potentialColliders)
   {
      // Plane origin/normal

      Point  pOrigin = any vertex from the current polygon;
      Vector pNormal = surface normal from the current polygon;

      // Determine the distance from the plane to the source

      Double pDist = intersect(source, -pNormal, pOrigin, pNormal);
      Point  sphereIntersectionPoint;
      Point  planeIntersectionPoint;

      // The radius of the ellipsoid (in the direction of pNormal)

      Vector directionalRadius = -pNormal * radiusVector;
      Double radius = length of directionalRadius;

      // Is the plane embedded?

      if (fabs(pDist) <= radius)
      {

         // Calculate the plane intersection point
       
         Vector temp = -pNormal with length set to pDist;
         planeIntersectionPoint = source + temp;

      }
      else
      {

         // Calculate the ellipsoid intersection point

         Vector temp = -pNormal with length set to radius;
         ellipsoidIntersectionPoint = source + temp;

         // Calculate the plane intersection point

         Ray    ray(sphereIntersectionPoint, Velocity);
         Double t = intersect(ellipsoidIntersectionPoint, Velocity, pOrigin, pNormal);

         // Calculate the plane intersection point

         Vector V = velocityVector with length set to t;
         planeIntersectionPoint = ellipsoidIntersectionPoint + V;
      }

 

      // Unless otherwise stated, our polygonIntersectionPoint is the
      // same point as planeIntersectionPoint

      Point  polygonIntersectionPoint = planeIntersectionPoint;

      // So… are they the same?

      if (planeIntersectionPoint is not within the current polygon)
      {
         polygonIntersectionPoint = nearest point on polygon's perimeter to planeIntersectionPoint;
      }

      // Invert the velocity vector

      Vector negativeVelocityVector = -velocityVector;

      // Using the polygonIntersectionPoint, we need to reverse-intersect
      // with the ellipsoid

      Double t = intersectEllipse(sourcePoint, radiusVector,
          polygonIntersectionPoint, negativeVelocityVector); 

      // Was there an intersection with the ellipsoid?

      if (t >= 0.0 && t <= distanceToTravel) 
      {

         Vector V = negativeVelocityVector with length set to t;

         // Where did we intersect the ellipsoid?

         Vector intersectionPoint = polygonIntersectionPoint + V;

         // Closest intersection thus far?

         if (firstTimeThrough || t < nearestDistance)
         {
            nearestDistance = t;
            nearestCollider = current collider;
            nearestIntersectionPoint = intersectionPoint;
            nearestPolygonIntersectionPoint =
            polygonIntersectionPoint;
            firstTimeThrough = false;
         }
      }
   }

       
   // If we never found a collision, we can safely move to the destination
   // and bail

   if (firstTimeThrough)
   {
      sourcePoint += velocityVector;
      return;
   }

   // Move to the nearest collision

   Vector V = velocityVector with length set to (nearestDistance - EPSILON);
   sourcePoint += V;

   // Determine the sliding plane (we do this now, because we're about to
   // change sourcePoint)

   Point  slidePlaneOrigin = nearestPolygonIntersectionPoint;
   Vector slidePlaneNormal = nearestPolygonIntersectionPoint - sourcePoint;

   // We now project the destination point onto the sliding plane

   Double time = intersect(destinationPoint, slidePlaneNormal,
         slidePlaneOrigin, slidePlaneNormal);

   Set length of slidePlaneNormal to time;

   Vector destinationProjectionNormal = slidePlaneNormal;

   Point  newDestinationPoint = destination + destinationProjectionNormal;

   // Generate the slide vector, which will become our new velocity vector
   // for the next iteration

   Vector newVelocityVector = newDestinationPoint –
      nearestPolygonIntersectionPoint;

   // Recursively slide (without adding gravity)

   collideWithWorld(sourcePoint, newVelocityVector);
}

Conclusion

If you have trouble with a topic in this document and you want more information on it (such as ray/ellipsoid intersections or clipping a polygon to a bounding box) don’t fret, there are plenty of references on the Internet. A good place to start is Paul Bourke’s Geometry Page (http://www.swin.edu.au/astronomy/pbourke/geometry/).

I would like to thank Shimon Shvartsbroit (a.k.a. “MasterBoy”) for his willingness to prove this algorithm in code (and along the way, helping me clarify and work out the kinks in this document.) Thanks to his effort, you can count on the fact that this document explains a technique that has been proven to work in practice. If you wish to contact Shimon, email him at cobra11@netvision.net.il or ICQ him at 14054887.

Happy coding,
Paul Nettle (a.k.a. “MidNight”)
midnight@graphicspapers.com

Discuss this article in the forums

Date this article was posted to GameDev.net: 5/26/2000
(Note that this date does not necessarily correspond to the date the article was written)

See Also:
Collision Detection

© 1999-2011 Gamedev.net. All rights reserved. Terms of Use Privacy Policy
Comments? Questions? Feedback? Click here!